1

次のような対称関係マトリックスがあるとします。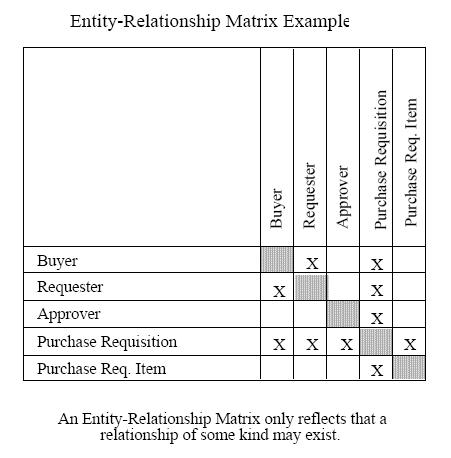

それぞれの「結果」が小さなコードであることを除いて。

私のシナリオ:Entity互いに「衝突」するオブジェクトがたくさんあります。各エンティティにはCollisionType値 (列挙型) があります。設計には、異なる CollisionType が互いに出会ったときにエンティティがどのように動作するかを説明する関係マトリックスが存在します。

新しい CollisionTypes を簡単に追加できるクリーンで高性能な方法で、関係を表現し、その上にロジックを実装するにはどうすればよいでしょうか? 私の考えでは、2D Switch ステートメントのように見えます。

例 (貧弱な) ソリューション:

void CollideEntities( Entity e1, Entity e2 ) {
    CollisionType t1 = e1.GetCollisionType();
    CollisionType t2 = e2.GetCollisionType();

    // perform basic logic based on t1 & t2
    if ( (t1 == COL_SOLID && t2 == COL_SQUISHY) || (t1 == COL_SQUISHY && t2 == COL_SOLID) ) {
        // do stuff..
    } else if ( (t1 == COL_SOLID && t2 == COL_DAMAGE) || (t1 == COL_DAMAGE && t2 == COL_SOLID) ) {
        // do other stuff..
    } // and so on...

}

多くの潜在的な解決策は明らかですが、特にクリーンで効率的で、新しいタイプを簡単に追加できるとは思えません...

4

2 に答える 2

2

私はそのようにはしません。キーが目的の動作を含むコマンドオブジェクトを検索するマップがあります。

もう1つの可能性は、Visitorパターン（別名「ダブルディスパッチ」）です。

于 2012-04-27T19:33:38.157 に答える
1

これを試して：

#include <vector>
#include <iostream>

class Symmetric_matrix {
  private:
    size_t size1;
    // The next should be <bool> rather than <int>,
    // but the writer's compiler objects.
    std::vector<int> outcomes;
  public:
    size_t size() const { return size1; }
    int &operator()(const size_t i, const size_t j) {
        const size_t a = i <= j ? i : j;
        const size_t b = i <= j ? j : i;
        return outcomes[(b*(b-1))/2 + a];
    }
    Symmetric_matrix(const size_t size0)
      : size1(size0), outcomes((size()*(size()-1))/2, false) {}
};

// Here is a test driver.
int main() {
    Symmetric_matrix sm(5);
    sm(0, 1) = true;
    sm(0, 3) = true;
    sm(1, 3) = true;
    sm(2, 3) = true;
    sm(3, 4) = true;
    std::cout << "buyer-approver      : " << sm(0, 2) << "\n";
    std::cout << "approver-buyer      : " << sm(2, 0) << "\n";
    std::cout << "approver-requisition: " << sm(2, 3) << "\n";
    std::cout << "requisition-approver: " << sm(3, 2) << "\n";
    return 0;
}

あなたの質問は興味深いものです。見てきたように、行列の上または下の三角形のみを保存する必要があり、両方を保存する必要はありません。

しかし(b*(b-1))/2、あなたは尋ねますか？答え: 0 + 1 + 2 + ... + (b-1) == (b*(b-1))/2 (試してみてください) という興味深い算術的事実から来ています。

もちろん、私のサンプル コードはいくらか改善される可能性があります。1 つには、何らかの理由で (アドバイスが必要です)、 を使用するとコードが失敗するstd::vector<bool>ため、回避策として を使用しstd::vector<int>ました。もう一つは、ケースの適切な取り扱いが含まれていないことi == jです。しかし、それがすることは、本質的な技術を伝えることです. あなたの裁量で詳細を記入することができます。

(更新:std::vector<bool>が失敗する理由が後でわかりました。std::vector<bool>ビットの配列として実装されているため失敗しますが、単一のビットはそれ自体のアドレスを持たないため左辺値operator()()にはなりません。巧妙なコーディングにより、戻り値を特別に定義された型のマニピュレータの場合、おそらく を変更せずに問題を解決することができますが、を使用したい場合は、メンバー関数main()を定義して使用するのがおそらく最も簡単です。)set()<bool>

于 2012-04-27T19:59:59.600 に答える