3

1 人が 8 面体のサイコロを 20 個振って、合計 8 の 20 乗の可能な結果が得られるゲームを想定します。特定のイベントが発生する確率を計算するには、イベントが発生する可能性のある方法の数を 8^20 で割ります。

値 3 のサイコロを正確に 5 つ得る方法の数を計算できます。(20 が 5 を選択) は、3 のオーダー数を示します。7^15 は、15 回のロールで値 3 を取得できない方法の数を示します。 .

number of ways to get exactly 5, 3's = (20 choose 5)*7^15.

答えは、文字列 3,3,3,3,3,0,0,0,0,0,0,0,0,0,0,0,0,0 を並べ替えることができる方法の数として見ることもできます,0,0 (20 は 5 を選択) にゼロの値の総数 (有効な値が 7 つあると仮定) 7^15 を掛けます (これは正しいです)。

  • 質問 1: 同じ値 (つまり、すべてのサイコロの値) のサイコロを正確に 5 つ得る方法の数を計算するにはどうすればよいですか? 注: 上記の最初の答えを単純に使用して bt 8 を掛けると、膨大な量の二重カウントが発生しますか?

    ケース (5 1's)、(5, 2's)、(5, 3's)、... (5's, 8) のそれぞれについて、それらを合計することができることを理解しています (より単純には 8*(5 1's) )。次に、オーバーラップ数の合計 (5 1) と (5 2)、(5 1) と (5 3)... (5 1) と (5, 2) と ... と (5, 8) を引きます。しかし、これは非常に面倒です。これを一般化して、多数のサンプルと多数のクラスにスケールアップします。

  • 同じ値のサイコロを 5つ以上得る方法の数を計算するにはどうすればよいですか?

    したがって、11111000000000000000 または 11110100000000000002 または 11111100000001110000 または 11011211222222223333 ですが、00001111222233334444 または 00051174134252 ではありません。

数学を説明するか、これをサポートするライブラリ（特にpythonモジュール）を指す答えを探しています。詳細と例の追加ポイント。

4

7 に答える 7

5

少し時間をかけてモンテカルロ シミュレーションを作成し、手動で計算しながら実行することをお勧めします。計算が完了する前にモンテカルロ シミュレーションが収束し、解を確認できることを願っています。

少し高速なオプションには、数学の問題用の SO クローンの作成が含まれる場合があります。

于 2009-07-29T19:53:20.943 に答える
3

重複カウントは、包含/除外の原則を使用して解決できます

私はそれが出てくると思います：

Choose(8,1)*P(one set of 5 Xs) 
- Choose(8,2)*P(a set of 5 Xs and a set of 5 Ys) 
+ Choose(8,3)*P(5 Xs, 5 Ys, 5 Zs) 
- Choose(8,4)*P(5 Xs, 5 Ys, 5 Zs, 5 As)

P(set of 5 Xs) = 20 Choose 5 * 7^15 / 8^20
P(5 Xs, 5 Ys) = 20 Choose 5,5 * 6^10 / 8^20

等々。これは、5,6,7..20 に適用された結果を単純に合計したかのように、「同じものが 5 つ以上ある」という問題を直接解決するものではありません。たとえば、1 が 10 個で 8 が 5 個の場合は、過大に数えます。

包含除外を再度適用して、その 2 番目の答えを見つけることができます。したがって、P(少なくとも 5 個の)=P(20 個の 1 セット)+ ... + (P(15 個の 1 セット) - 7*P(5 個のサイコロから 5 個のセット)) + (((P(1 個のサイコロのセット) of 14) - 7*P (6 から 5 の 1 セット) - 7*P (6 から 6 の 1 セット)) そのためのソース コードを考え出すことは、それ自体がより困難であることを証明しています。

于 2009-07-29T19:48:39.393 に答える
2

この問題を一般化する (正確な式を取得する) 必要がある場合、この問題は非常に困難です。

とにかく、アルゴリズムを説明しましょう。知りたい場合

同じ値のサイコロをちょうど 5 個得る方法の数

以前の問題を言い換える必要があります。

値 3 のサイコロを正確に 5 個取得する方法の数を計算し、かつ他の値を正確に 5 回繰り返すことはできません

簡単にするために、関数 F(20,8,5) (5 つのサイコロ、すべての値) を最初の答えと呼び、F(20,8,5,3) (5 つのサイコロ、値 3) を 2 番目の答えと呼びましょう。F(20,8,5) = F(20,8,5,3) * 8 + (複数の値が 5 回繰り返されるイベント)

F(20,8,5,3) を取得できれば、かなり単純なはずですよね? うーん…あんまり…

最初に、いくつかの変数を定義しましょう: X1,X2,X3...,Xi 、ここで Xi = サイコロ i を取得する回数

それで：

F(20,8,5)/20^8 = P(X1=5 or X2=5 or ... or X8=5, with R=20(rolls) and N=8(dice number))

、P(ステートメント) は、確率を記述する標準的な方法です。

私たちは続けます：

F(20,8,5,3)/20^8 = P(X3=5 and X1<>5 and ... and X8<>5, R=20, N=8) 
F(20,8,5,3)/20^8 = 1 - P(X1=5 or X2=5 or X4=5 or X5=5 or X6=5 or X7=5 or X8=5, R=15, N=7)  
F(20,8,5,3)/20^8 = 1 - F(15,7,5)/7^15

再帰的に:

F(15,8,5) = F(15,7,5,1) * 7  
P(X1=5 or X2=5 or X4=5 or X5=5 or X6=5 or X7=5 or X8=5, R=15, N=7) = P(X1=5 and X2<>5 and X4<>5 and .. and X8<>5. R=15, N=7) * 7

F(15,7,5,1)/7^15 = 1 - F(10,6,5)/6^10 F(10,6,5) = F(10,6,5,2) * 6

F(10,6,5,2)/6^10 = 1 - F(5,5,5)/5^5
F(5,5,5) = F(5,5,5,4) * 5

それでは... F(5,5,5,4) は、他のサイコロが 5 回繰り返されないように、5 回のロールで値 4 のサイコロを 5 つ得る方法の数です。合計 5^5 のうち、1 つの方法しかありません。確率は 1/5^5 です。

F(5,5,5) は、5 回のロールで (5 つの値から) 任意の値の 5 つのサイコロを取得する方法の数です。明らかに 5 です。確率は 5/5^5 = 1/5^4 です。

F(10,6,5,2) は、10 回のロールで値 2 の 5 つのサイコロを取得する方法の数です。たとえば、他のサイコロが 5 回繰り返されることはありません。F(10,6,5,2) = (1-F(5,5,5)/5^5) * 6^10 = (1-1/5^4) * 6^10

うーん...どこかで間違っているかもしれないと思いますが、とにかく、あなたはその考えを理解します. アルゴリズムをわかりやすくすることができれば幸いです。

編集: いくつかのチェックを行ったところ、複数の値が正確に 5 回繰り返される場合、いくつかのケースを追加する必要があることに気付きました。あなたはその部分を解決する時間がありません...

于 2009-07-29T21:38:14.467 に答える
2

i 面のサイコロの合計の正確な確率分布 Fs,i は、1 つのサイコロの確率分布とそれ自体の繰り返し畳み込みとして計算できます。

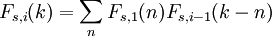
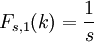代替テキスト

代替テキスト すべての場合はどこで 、代替テキストそれ以外の場合は 0 です。

http://en.wikipedia.org/wiki/Dice

于 2009-07-29T19:12:59.027 に答える
1

n 個のイベントで x 回出現する式を次のように使用できると思います。

P = 確率^n * (n!/((n - x)!x!))

したがって、最終結果は 0 から n までの結果の合計になります。

それを 1 つのステップにまとめて、それほど面倒ではない簡単な方法は本当にありません。このようにして、式もコード内に記述されます。ただし、独自の階乗法を作成する必要がある場合があります。

  float calculateProbability(int tosses, int atLeastNumber) {
    float atLeastProbability = 0;
    float eventProbability = Math.pow( 1.0/8.0, tosses);
    int nFactorial = factorial(tosses);

    for ( i = 1; i <= atLeastNumber; i++) {
      atLeastProbability += eventProbability * (nFactorial / (factorial(tosses - i) * factorial(i) );
    }
  }
于 2009-07-29T19:52:36.000 に答える
1

再帰的な解決策:

Prob_same_value(n) = Prob_same_value(n-1) * (1 - Prob_noone_rolling_that_value(N-(n-1)))
于 2009-07-29T19:29:02.953 に答える
1

これが私が考えていることです...

サイコロが 5 つしかない場合、欲しいものを手に入れる方法は 8 つしかありません。

これらの 8 つの方法のそれぞれについて、他の 15 個のサイコロのすべての可能な組み合わせが機能します。

だから - 答えは (8 * 8 15) / 8 20だと思います

（少なくとも5つの同じ答え。）

于 2009-07-29T19:44:56.843 に答える