5

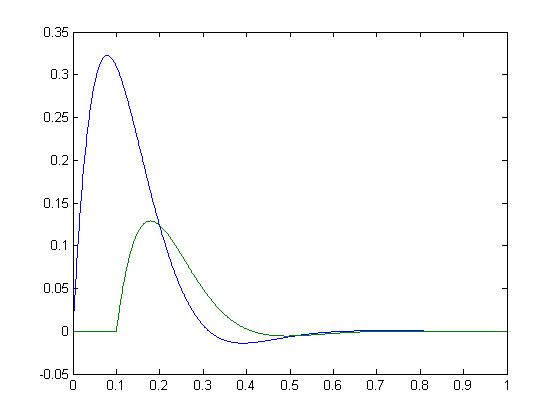
前もって少し冗長であることをお詫びします。背景の巨大なジャンボをすべてスキップしたい場合は、下の私の質問をご覧ください。

これは、2 つの 1D (時間依存) 信号を比較する方法について以前に投稿した質問のフォローアップです。私が得た答えの 1 つは、相互相関関数 (MATLAB では xcorr) を使用することでした。

背景情報

少し背景情報が役に立つかもしれません。私は独立成分分析アルゴリズムを実装しようとしています。私の非公式なテストの 1 つは、(1) (a) 2 つのランダムなベクトル (1x1000) を生成し、(b) ベクトルを 2x1000 の行列 ("S" と呼ばれる) に結合し、これに 2x2 の混合を掛けることでテスト ケースを作成することです。行列 (「A」と呼びます) を入力して、新しい行列 (「T」と呼びましょう) を提供します。

要約すると、T = A * S

(2) 次に、ICA アルゴリズムを実行して混合行列の逆行列 ("W" と呼ばれる) を生成します。(3) "T" に "W" を掛けて、(できれば) 元の信号行列 (と呼ばれる) を再構成します。 "バツ"）

要約すると、X = W * T

(4) 「S」と「X」を比較したい。"S" と "X" は 2x1000 ですが、それぞれ 1x1000 の と を単純に比較してS(1,:)1D信号にしています。（これらのベクトルが互いに比較するのに適切なベクトルであることを確認し、信号を正規化する別のステップがあります）。X(1,:)S(2,:)X(2,:)

したがって、私の現在の困惑は、にどれだけ近いかを「評価」する方法であり、同様にtoにもS(1,:)一致します。X(1,:)S(2,:)X(2,:)

これまでのところ、次のようなものを使用しています：r1 = max(abs(xcorr(S(1,:), X(1,:)))

私の質問

相互相関関数を使用することが 2 つのシグナルの類似性を比較する有効な方法であると仮定すると、シグナルの類似性を評価するのに適した R 値はどれでしょうか? ウィキペディアは、これは非常に主観的な領域であると述べているため、この分野の経験がある可能性のある人々のより良い判断に委ねます.

お気づきかもしれませんが、私は EE/DSP/統計のバックグラウンドをまったく持っていません (私は医学生です) ので、現在、一種の「火によるバプテスマ」を受けています。私が得ることができる助け。ありがとう！

4

6 に答える 6

12

（編集： R値に関する質問に直接答える限り、以下を参照してください）

これにアプローチする1つの方法は、相互相関を使用することです。振幅を正規化し、遅延を補正する必要があることに注意してください。信号S1があり、信号S2の形状は同じですが、振幅が半分で3サンプル遅延している場合でも、完全に相関しています。

例えば：

>> t = 0:0.001:1;
>> y = @(t) sin(10*t).*exp(-10*t).*(t > 0);
>> S1 = y(t);
>> S2 = 0.4*y(t-0.1);
>> plot(t,S1,t,S2);

代替テキスト

これらは完全な相関係数を持っている必要があります。これを計算する方法は、最大の相互相関を使用することです。

>> f = @(S1,S2) max(xcorr(S1,S2));

f = 

    @(S1,S2) max(xcorr(S1,S2))

>>  disp(f(S1,S1)); disp(f(S2,S2)); disp(f(S1,S2));
   12.5000

    2.0000

    5.0000

の最大値はxcorr()、信号間の時間遅延を処理します。振幅の補正に関しては、信号を正規化して自己相互相関が1.0になるようにするか、同等のステップを次のように折りたたむことができます。

ρ2 =f（S1、S2）2 /（f（S1、S1）* f（S2、S2）;

この場合、ρ2 = 5 * 5 /（12.5 * 2）= 1.0

ρ自体を解くことができます。つまり、ρ= f（S1、S2）/ sqrt（f（S1、S1）* f（S2、S2））ですが、1.0と-1.0の両方が完全に相関している（-1.0反対の符号があります）

あなたの信号でそれを試してみてください！

受け入れ/拒否に使用するしきい値に関しては、実際には、信号の種類によって異なります。0.9以上はかなり良いですが、誤解を招く可能性があります。相関バージョンを差し引いた後に得られる残差信号を調べることを検討します。これを行うには、xcorr（）の最大値の時間インデックスを確認します。

>> t = 0:0.001:1;
>> y = @(a,t) sin(a*t).*exp(-a*t).*(t > 0);
>> S1=y(10,t);
>> S2=0.4*y(9,t-0.1);
>> f(S1,S2)/sqrt(f(S1,S1)*f(S2,S2))

ans =

    0.9959

これは、相関関係にはかなり良いように見えます。しかし、S1のスケーリング/シフトされた倍数でS2をフィッティングしてみましょう。

>> [A,i]=max(xcorr(S1,S2)); tshift = i-length(S1);
>> S2fit = zeros(size(S2)); S2fit(1-tshift:end) = A/f(S1,S1)*S1(1:end+tshift);
>> plot(t,[S2; S2fit]); % fit S2 using S1 as a basis

代替テキスト

>> plot(t,[S2-S2fit]);  % residual

代替テキスト

残差にはある程度のエネルギーがあります。どれだけの感触を得るために、あなたはこれを使うことができます：

>> S2res=S2-S2fit;
>> dot(S2res,S2res)/dot(S2,S2)

ans =

    0.0081

>> sqrt(dot(S2res,S2res)/dot(S2,S2))

ans =

    0.0900

これは、残差が元の信号S2のエネルギーの約0.81％（二乗平均平方根振幅の9％）を持っていることを示しています。（1D信号とそれ自体の内積は、常にその信号とそれ自体の相互相関の最大値に等しくなります。）

2つの信号が互いにどれほど似ているかを答えるための特効薬はないと思いますが、あなたの状況に当てはまるかもしれないいくつかのアイデアを提供できれば幸いです。

于 2009-08-19T13:08:38.527 に答える
1

これは完全な推測ですが、 max(abs(xcorr(S(1,:),X(1,:))) > 0.8 は成功を意味すると推測しています。好奇心から、max(abs(xcorr(S(1,:),X(2,:)))) に対してどのような値が得られますか?

アルゴリズムを検証するもう 1 つの方法は、A と W を比較することです。W が正しく計算されれば、A^-1 になるはずです。A*W-私|? のトレースで正規化する必要があるかもしれませんA*W。

元の質問に戻りますが、私は DSP のバックグラウンドを持っているので、かなりノイズのない信号を扱うことができます。それは生物学で得られる贅沢ではないことを私は理解しています:)したがって、私の0.8の推測は非常に楽観的かもしれません. おそらく、相互相関を正確に使用していなくても、あなたの分野のいくつかの文献を見ると役立つかもしれません。

于 2009-08-17T21:38:45.940 に答える
1

適切な出発点は、各信号の自己相関を計算することによって、完全な一致がどのように見えるかを把握することです(つまり、各信号とそれ自体の「相互相関」を実行します)。

于 2009-08-17T20:18:36.087 に答える
1

通常、そのような場合、人々は「他人受入率」と「本人拒否率」について話します。最初のものは、アルゴリズムが類似していない信号に対して「類似」と言う回数を記述し、2 番目のものはその逆です。

したがって、しきい値の選択は、これらの基準間のトレードオフになります。FAR=0 にするにはしきい値を 1 に、FRR=0 にするにはしきい値を -1 にします。

したがって、おそらく、FAR と FRR の間のどのトレードオフが自分の状況で許容できるかを決定する必要があり、これによりしきい値の適切な値が得られます。

数学的には、これはさまざまな方法で表現できます。いくつかの例: 1. レートの一部を許容値に固定し、他のレートを最小化する 2. max(FRR,FAR) を最小化する 3. FRR+b FARを最小化する

于 2009-08-18T09:11:17.107 に答える
0

結果は主観的なものになることに同意します。要素ごとの差の二乗の合計を含む何かには、何らかの価値があります。2つの同一の配列は、その形式で値0を返します。次に、どの値が「不良」になるかを決定する必要があります。「それほど悪くない」2つの異なるベクトルを作成し、それらの相互相関係数をガイドとして使用します。

（括弧内：1または-1が大きく、0がひどい相関係数を実行している場合、生物統計学者から、実際の値0.7は非常に良いと言われています。これは正確にはあなたがしていることではありませんが、相関係数に関するコメントは以前に出てきました。）

于 2009-08-17T20:30:48.510 に答える
0

それらは等しくなければならないので、相関係数は .99 から 1 の間で高くなるはずです。計算から max 関数と abs 関数も除外します。

編集: 話すのが早すぎました。相互相関と相関係数を混同しましたが、これはまったく別のものです。私の答えはあまり価値がないかもしれません。

于 2009-08-17T18:23:41.700 に答える