アドバイスが必要です。Flow Free に似たゲームを開発しています。ゲームボードはグリッドと色付きのドットで構成されており、ユーザーは同じ色のドットを他の線と重なることなく接続し、ボード内のすべての空きスペースを使い果たす必要があります。
私の質問は、レベルの作成についてです。レベルをランダムに生成したい (そして、プレイヤーにヒントを与えることができるように、少なくともそれ自体を解決できるようにする必要があります) と、どのアルゴリズムを使用するかについて困っています。助言がありますか？
注: 画像は Flow Free の目的を示しており、私が開発しているものと同じ目的です。
ご協力いただきありがとうございます。:)
単純で管理しやすいアルゴリズムのペアを使用して問題を解決することを検討してください。1 つは単純な解決済みのボードを確実に作成するアルゴリズムで、もう 1 つはフローを再配置して単純なボードをより複雑にするアルゴリズムです。
xグリッドnでフローを使用している場合、最初の部分である単純な事前解決済みボードの作成は簡単です(必要に応じて) 。nn
または、独自の手作りのスターター ボードを提供して、2 番目の部分に渡すこともできます。この段階の唯一の目標は、有効なボードを構築することです。それが些細なことや事前に決められていることであっても、単純にする価値があります。
フローを再配置する 2 番目の部分では、各フローをループして、どのフローが隣接するフローと連携して拡大および縮小できるかを確認します。
fます。fは、すぐに縮小できないため、次の反復にスキップしfます。f別のフローのドットの隣にあるg場合 (選択するものが複数ある場合gは、ランダムに 1 つ選択します)...
fします (つまり、尾に向かって 1 マス歩きます)。fは 1 マス短くなり、空のマスがあります。（パズルは現在未解決です。）gによって空けられた空の正方形にから隣接するドットを移動しfます。gのドットが移動した空の四角形ができました。gます。gこの反復の開始時よりも 1 マス長くなりました。（パズルも解決済みに戻ります。）fの末尾のドットについて、前の手順を繰り返します。現状のアプローチには制限があります (ドットは常に隣接します) が、簡単に拡張できます。
fスペースを他のフローと交換するよりトリッキーな方法を探します...ここでの全体的なソリューションは、おそらくあなたが目指している理想的なソリューションにはほど遠いものですが、これで 2 つの単純なアルゴリズムをさらに具体化して、1 つの大規模で包括的なアルゴリズムの役割を果たすことができます。結局のところ、このアプローチは管理しやすく、不可解ではなく、簡単に調整できると思います。そして、何よりも、始めるのに適した場所だと思います.
更新:上記の手順に基づいて概念実証をコーディングしました。以下の最初の 5x5 グリッドから始めて、このプロセスにより、後続の 5 つの異なるボードが作成されました。興味深いものもあれば、そうでないものもありますが、1 つの既知のソリューションで常に有効です。
出発点
5 つのランダムな結果(スクリーンショットの位置がずれていて申し訳ありません)
そして、適切な測定のためにランダムな8x8。出発点は、上記と同じ単純な列アプローチでした。
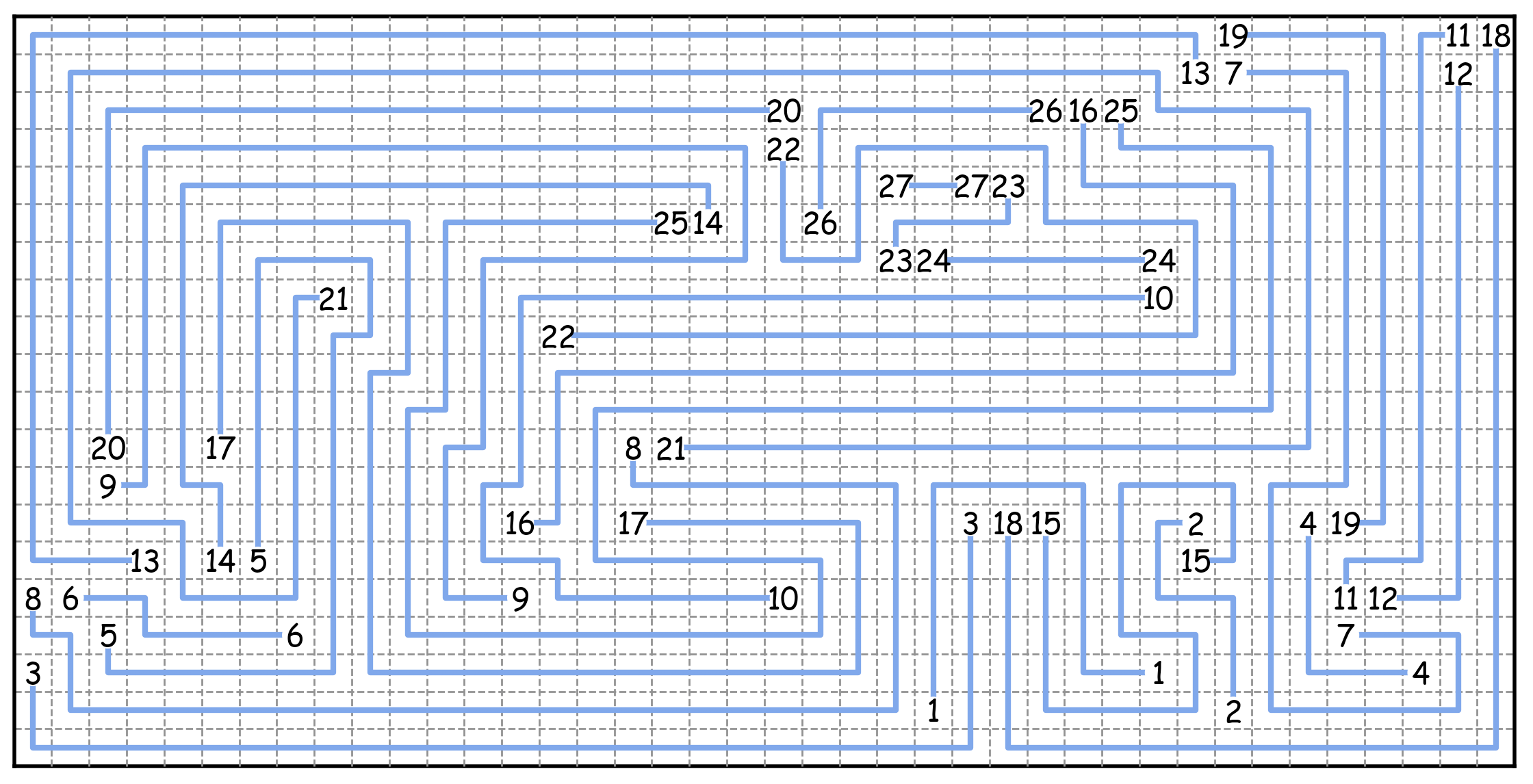
このようなレベルを作成する最も簡単な方法は、それを解決する方法を見つけることです。このようにして、基本的にランダムな開始構成を生成し、それを解決しようとすることで有効なレベルであるかどうかを判断できます。これにより、最も多様なレベルが生成されます。
また、別の方法でレベルを生成する方法を見つけたとしても、この解決アルゴリズムを適用して、生成されたレベルが適切であることを証明する必要があります ;)
ボードのサイズが NxN セルで、N 色も利用できる場合、考えられるすべての構成を (開始ノードと終了ノード間の実際のパスを形成するかどうかに関係なく) 力ずくで列挙すると、次のようになります。
そう、
つまり、可能な組み合わせの数は最初はかなり多いのですが、ボードを大きくし始めると途方もなく速く増えます。
明らかに、構成の数をできるだけ減らすようにする必要があります。これを行う 1 つの方法は、各色の開始セルと終了セルの間の最小距離 ("dMin") を考慮することです。少なくとも、その色のセルがこれだけ多く存在する必要があることがわかっています。最小距離の計算は、単純なフラッド フィルまたはダイクストラのアルゴリズムで行うことができます。(注意: この次のセクション全体では、セルの数についてのみ説明していますが、それらの場所については何も述べていません)
あなたの例では、これは（開始セルと終了セルを数えない）ことを意味します
dMin(orange) = 1
dMin(red) = 1
dMin(green) = 5
dMin(yellow) = 3
dMin(blue) = 5
これは、まだ色が決定されていない 15 個のセルのうち、少なくとも 1 個のオレンジ、1 個の赤、5 個の緑、3 個の黄、および 5 個の青のセルが必要であり、合計 15 個のセルになることを意味します。この特定の例では、各色の開始セルと終了セルを最短パス (の 1 つ) で接続すると、ボード全体が塗りつぶされます。つまり、ボードを最短パスで塗りつぶした後、色のないセルは残りません。(これは「運」と考えるべきです。ボードのすべての開始構成がこれを引き起こすわけではありません)。
通常、このステップの後、自由に色付けできる多数のセルができます。この数を U と呼びましょう。N=5 の場合、
U = 15 - (dMin(orange) + dMin(red) + dMin(green) + dMin(yellow) + dMin(blue))
これらのセルは任意の色を取ることができるため、特定の色を持つことができるセルの最大数を決定することもできます。
dMax(orange) = dMin(orange) + U
dMax(red) = dMin(red) + U
dMax(green) = dMin(green) + U
dMax(yellow) = dMin(yellow) + U
dMax(blue) = dMin(blue) + U
(この特定の例では、U=0 であるため、色ごとのセルの最小数は最大数でもあります)。
これらの色の制約を使用して可能なすべての組み合わせを力ずくで列挙すると、心配する組み合わせがはるかに少なくなります。より具体的には、この特定の例では次のようになります。
15! / (1! * 1! * 5! * 3! * 5!)
= 1307674368000 / 86400
= 15135120 combinations left, about a factor 2000 less.
ただし、これでも実際のパスはわかりません。したがって、より良いアイデアは、バックトラッキング検索を使用することです。この場合、各色を順番に処理し、次のすべてのパスを見つけようとします。
2 番目の基準は、色ごとに報告されるパスの数を減らします。これにより、試行されるパスの総数が大幅に削減されます (組み合わせ効果による)。
擬似コード:
function SolveLevel(initialBoard of size NxN)
{
foreach(colour on initialBoard)
{
Find startCell(colour) and endCell(colour)
minDistance(colour) = Length(ShortestPath(initialBoard, startCell(colour), endCell(colour)))
}
//Determine the number of uncoloured cells remaining after all shortest paths have been applied.
U = N^(N^2 - 2N) - (Sum of all minDistances)
firstColour = GetFirstColour(initialBoard)
ExplorePathsForColour(
initialBoard,
firstColour,
startCell(firstColour),
endCell(firstColour),
minDistance(firstColour),
U)
}
}
function ExplorePathsForColour(board, colour, startCell, endCell, minDistance, nrOfUncolouredCells)
{
maxDistance = minDistance + nrOfUncolouredCells
paths = FindAllPaths(board, colour, startCell, endCell, minDistance, maxDistance)
foreach(path in paths)
{
//Render all cells in 'path' on a copy of the board
boardCopy = Copy(board)
boardCopy = ApplyPath(boardCopy, path)
uRemaining = nrOfUncolouredCells - (Length(path) - minDistance)
//Recursively explore all paths for the next colour.
nextColour = NextColour(board, colour)
if(nextColour exists)
{
ExplorePathsForColour(
boardCopy,
nextColour,
startCell(nextColour),
endCell(nextColour),
minDistance(nextColour),
uRemaining)
}
else
{
//No more colours remaining to draw
if(uRemaining == 0)
{
//No more uncoloured cells remaining
Report boardCopy as a result
}
}
}
}
これにより、FindAllPaths(board, color, startCell, endCell, minDistance, maxDistance) のみが実装されます。ここで注意が必要なのは、最短パスを検索するのではなく、minDistance と maxDistance によって決定される範囲内にあるすべてのパスを検索することです。したがって、ダイクストラや A* だけを使用することはできません。それらは各セルへの最短経路のみを記録し、可能な迂回経路は記録しないからです。
これらのパスを見つける 1 つの方法は、ボードに多次元配列を使用することです。この場合、各セルは複数のウェイポイントを格納でき、ウェイポイントはペア (前のウェイポイント、原点までの距離) として定義されます。目的地に到達した後にパス全体を再構築できるようにするには、前のウェイポイントが必要であり、原点までの距離により、maxDistance を超えることはできません。
次に、startCell から外側に向かってフラッド フィルのような探索を使用して、すべてのパスを見つけることができます。この場合、特定のセルについて、色付けされていない、または現在の色と同じ色の隣接する各セルが再帰的に探索されます (形成されるものを除く)。 endCell に到達するか maxDistance を超えるまで、原点への現在のパス)。
この戦略の改善点は、startCell から外側の endCell まで探索するのではなく、Floor(maxDistance / 2) と Ceil(maxDistance / 2) をそれぞれの最大距離。maxDistance の値が大きい場合、探索されるセルの数が 2 * maxDistance^2 から maxDistance^2 に減少します。
更新された回答:「デュアル パズル」のアイデアを使用して、新しいジェネレーターを実装しました。これにより、私が知っている以前の方法よりもはるかにまばらで高品質のパズルが可能になります。コードはgithub にあります。それがどのように機能するかについてもっと詳しく書きたいと思いますが、ここにパズルの例があります：
古い回答: numberlink のソルバーとジェネレーター に次のアルゴリズムを実装しました。ほとんどの「ハードコア」なナンバーリンク アプリやパズルでは通常、パスが自分自身に触れてはならないというルールが適用されます。
私の numberlink 形式は、数字の代わりに ASCII 文字を使用しています。次に例を示します。
$ bin/numberlink --generate=35x20
Warning: Including non-standard characters in puzzle
35 20
....bcd.......efg...i......i......j
.kka........l....hm.n....n.o.......
.b...q..q...l..r.....h.....t..uvvu.
....w.....d.e..xx....m.yy..t.......
..z.w.A....A....r.s....BB.....p....
.D.........E.F..F.G...H.........IC.
.z.D...JKL.......g....G..N.j.......
P...a....L.QQ.RR...N....s.....S.T..
U........K......V...............T..
WW...X.......Z0..M.................
1....X...23..Z0..........M....44...
5.......Y..Y....6.........C.......p
5...P...2..3..6..VH.......O.S..99.I
........E.!!......o...."....O..$$.%
.U..&&..J.\\.(.)......8...*.......+
..1.......,..-...(/:.."...;;.%+....
..c<<.==........)./..8>>.*.?......@
.[..[....]........:..........?..^..
..._.._.f...,......-.`..`.7.^......
{{......].....|....|....7.......@..
そして、ここでソルバー (同じシード) で実行します。
$ bin/numberlink --generate=35x20 | bin/numberlink --tubes
Found a solution!
┌──┐bcd───┐┌──efg┌─┐i──────i┌─────j
│kka│└───┐││l┌─┘│hm│n────n┌o│┌────┐
│b──┘q──q│││l│┌r└┐│└─h┌──┐│t││uvvu│
└──┐w┌───┘d└e││xx│└──m│yy││t││└──┘│
┌─z│w│A────A┌┘└─r│s───┘BB││┌┘└p┌─┐│
│D┐└┐│┌────E│F──F│G──┐H┐┌┘││┌──┘IC│
└z└D│││JKL┌─┘┌──┐g┌─┐└G││N│j│┌─┐└┐│
P──┐a││││L│QQ│RR└┐│N└──┘s││┌┘│S│T││
U─┐│┌┘││└K└─┐└─┐V││└─────┘││┌┘││T││
WW│││X││┌──┐│Z0││M│┌──────┘││┌┘└┐││
1┐│││X│││23││Z0│└┐││┌────M┌┘││44│││
5│││└┐││Y││Y│┌─┘6││││┌───┐C┌┘│┌─┘│p
5││└P│││2┘└3││6─┘VH│││┌─┐│O┘S┘│99└I
┌┘│┌─┘││E┐!!│└───┐o┘│││"│└─┐O─┘$$┌%
│U┘│&&│└J│\\│(┐)┐└──┘│8││┌*└┐┌───┘+
└─1└─┐└──┘,┐│-└┐│(/:┌┘"┘││;;│%+───┘
┌─c<<│==┌─┐││└┐│)│/││8>>│*┌?│┌───┐@
│[──[└─┐│]││└┐│└─┘:┘│└──┘┌┘┌┘?┌─^││
└─┐_──_│f││└,│└────-│`──`│7┘^─┘┌─┘│
{{└────┘]┘└──┘|────|└───7└─────┘@─┘
ステップ (4) を、隣接する 2 つのパスを繰り返しランダムにマージする関数に置き換えることをテストしました。しかし、それははるかに密度の高いパズルのゲームであり、上記は難しすぎるほど密度が高すぎるとすでに思っています。
これは、私が生成したさまざまなサイズの問題のリストです: https://github.com/thomasahle/numberlink/blob/master/puzzles/inputs3
これは 2 つのステップで行う必要があると思います。ステップ 1) すべてのポイントを接続する交差しないパスのセットを見つけ、次に 2) それらのパスを成長/シフトしてボード全体を埋めます。
ステップ 1 に関する私の考えは、すべてのポイントで同時にダイクストラのようなアルゴリズムを実行し、パスを一緒に成長させることです。ダイクストラと同様に、ヒューリスティックを使用して次にどのノードを検索するかを選択して、各ポイントからフラッド フィルアウトする必要があると思います (私の勘では、最初に自由度が最も低いポイントを選択し、次に距離によって、いいもの）。ダイクストラとは大きく異なりますが、同じノードに成長しようとする複数のパスがある場合、バックトラックする必要があると思います。(もちろん、これは大きなマップではかなり問題になる可能性がありますが、上記のような小さなマップでは大した問題ではない可能性があります。)
上記のアルゴリズムを開始する前に、主に必要なバックトラックの数を減らすために、いくつかのより簡単なパスを解決することもできます。具体的には、ボードの端に沿ってポイント間のトレースを作成できれば、それらの 2 つのポイントをそのように接続しても他のパスに干渉しないことが保証されます。方程式。次に、ボードの境界または既存のパスの境界に沿ってトレースすることにより、これらの「すばやく簡単な」パスがすべて見つかるまで、これをさらに繰り返すことができます。そのアルゴリズムは実際には上記の例のボードを完全に解決しますが、他の場所では間違いなく失敗します.. それでも、実行するのは非常に安価であり、前のアルゴリズムの検索時間を短縮します.
あるいは
ポイントの各セット間で実際のダイクストラのアルゴリズムを実行し、最初に最も近いポイントをパスします (またはランダムな順序で数回試行します)。これはおそらくかなりの数のケースで機能し、失敗した場合は単純にマップを破棄して新しいマップを生成します。
ステップ 1 を解決したら、ステップ 2 は簡単になりますが、必ずしも簡単ではありません。パスを拡張するには、パスを外側に拡張する必要があると思います (最初に壁に最も近いパス、壁に向かって拡張し、次に他の内側のパスを外側に拡張するなど)。成長するには、コーナーを反転させ、隣接する空の正方形のペアに拡張するという2つの基本的な操作があると思います..つまり、次のような行がある場合
.v<<.
v<...
v....
v....
最初に、コーナーを反転してエッジ スペースを埋めます。
v<<<.
v....
v....
v....
次に、オープン スペースの隣接するペアに拡張する必要があります。
v<<v.
v.^<.
v....
v....
v<<v.
>v^<.
v<...
v....
等..
私が概説したことは、解決策が存在する場合に解決策を保証するものではありませんが、存在する場合はほとんどの場合、解決策を見つけることができるはずであり、マップに解決策がない場合、またはアルゴリズムが失敗した場合に注意してください。 1つ見つけたら、マップを捨てて、別のマップを試してください:)