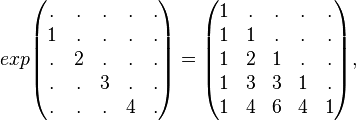c++ - Pascals Triangle by recursion

Question

Note : My Class Teacher gave me this question as an assignment... I am not asked to do it but please tell me how to do it with recursion

Binomial coefficients can be calculated using Pascal's triangle:

            1                   n = 0
         1     1
      1     2     1
   1     3     3     1
1     4     6     4     1       n = 4

Each new level of the triangle has 1's on the ends; the interior numbers are the sums of the two numbers above them.

Task: Write a program that includes a recursive function to produce a list of binomial coefficients for the power n using the Pascal's triangle technique. For example,

Input = 2 Output = 1 2 1

Input = 4 Output = 1 4 6 4 1

done this So Far but tell me how to do this with recursion...

#include<stdio.h>

int main()    
{
  int length,i,j,k;
//Accepting length from user
  printf("Enter the length of pascal's triangle : ");
  scanf("%d",&length);
//Printing the pascal's triangle
  for(i=1;i<=length;i++)
  {
      for(j=1;j<=length-i;j++)      
      printf(" ");
      for(k=1;k<i;k++)
          printf("%d",k);
      for(k=i;k>=1;k--)
          printf("%d",k);
      printf("\n");
  }
  return 0;    
}

Answer 1

Method 1:

Simplest way is to use the binomial coefficients. With this method, you have 1 recursive method:

// Here is your recursive function!
// Ok ok, that's cheating...
unsigned int fact(unsigned int n)
{
    if(n == 0) return 1;
    else return n * fact(n - 1);
}

unsigned int binom(unsigned int n, unsigned k)
{
    // Not very optimized (useless multiplications)
    // But that's not really a problem: the number will overflow
    // way earlier than you will notice any performance problem...
    return fact(n) / (fact(k) * fact(n - k));
}

std::vector<unsigned int> pascal(unsigned n)
{
    std::vector<unsigned int> res;
    for(unsigned int k = 0; k <= n; k++)
        res.push_back(binom(n,k));
    return res;
}

Live example.

Method 2:

This method use the construction with the formulae:

Here, the only function is recursive and compute one line at a time, storing these result in an array (in order to cache results).

std::vector<unsigned int> pascal(unsigned int n)
{
    // This variable is static, to cache results.
    // Not a problem, as long as mathematics do not change between two calls,
    // which is unlikely to happen, hopefully.
    static std::vector<std::vector<unsigned int> > triangle;

    if(triangle.size() <= n)
    {
        // Compute for i = last to n-1
        while(triangle.size() != n)
            pascal(triangle.size());

        // Compute for n
        if(n == 0)
            triangle.push_back(std::vector<unsigned int>(1,1));
        else
        {
            std::vector<unsigned int> result(n + 1, 0);
            for(unsigned int k = 0; k <= n; k++)
            {
                unsigned int l = (k > 0 ? triangle[n - 1][k - 1] : 0);
                unsigned int r = (k < n ? triangle[n - 1][k] : 0);
                result[k] = l + r;
            }
            triangle.push_back(result);
        }
    }

    // Finish
    return triangle[n];
}

Live example.

Others methods:

There are some other exotic methods, using the properties of the triangle. You can also use the matrix way to generate it:

No code for it, as it would require a lot of base code (matrices, exponential of matrix, etc...), and it is not really recursive.

On a side note, I think this problem is absolutely not the right problem to teach recursion. There are a lot of better cases for it.