問題/問題のコミック: http://xkcd.com/287/
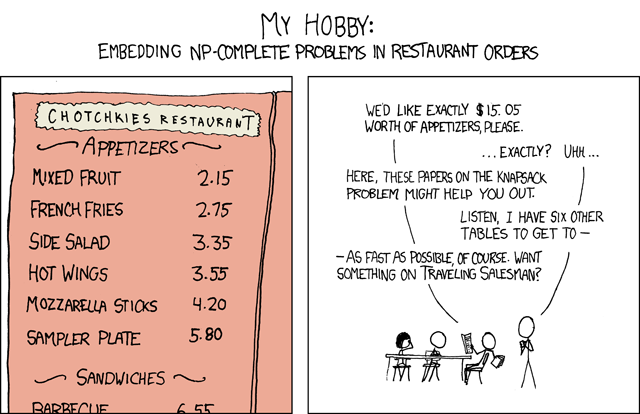
これが最善の方法かどうかはわかりませんが、これまでのところ私が思いついた方法は次のとおりです。私は CFML を使用していますが、誰でも読めるはずです。
<cffunction name="testCombo" returntype="boolean">
<cfargument name="currentCombo" type="string" required="true" />
<cfargument name="currentTotal" type="numeric" required="true" />
<cfargument name="apps" type="array" required="true" />
<cfset var a = 0 />
<cfset var found = false />
<cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">
<cfset arguments.currentCombo = listAppend(arguments.currentCombo, arguments.apps[a].name) />
<cfset arguments.currentTotal = arguments.currentTotal + arguments.apps[a].cost />
<cfif arguments.currentTotal eq 15.05>
<!--- print current combo --->
<cfoutput><strong>#arguments.currentCombo# = 15.05</strong></cfoutput><br />
<cfreturn true />
<cfelseif arguments.currentTotal gt 15.05>
<cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />
<cfreturn false />
<cfelse>
<!--- less than 15.05 --->
<cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />
<cfset found = testCombo(arguments.currentCombo, arguments.currentTotal, arguments.apps) />
</cfif>
</cfloop>
</cffunction>
<cfset mf = {name="Mixed Fruit", cost=2.15} />
<cfset ff = {name="French Fries", cost=2.75} />
<cfset ss = {name="side salad", cost=3.35} />
<cfset hw = {name="hot wings", cost=3.55} />
<cfset ms = {name="moz sticks", cost=4.20} />
<cfset sp = {name="sampler plate", cost=5.80} />
<cfset apps = [ mf, ff, ss, hw, ms, sp ] />
<cfloop from="1" to="6" index="b">
<cfoutput>#testCombo(apps[b].name, apps[b].cost, apps)#</cfoutput>
</cfloop>
上記のコードは、$15.05 になる唯一の組み合わせはミックス フルーツの 7 注文であり、完了するまでに testCombo 関数を 232 回実行する必要があることを示しています。
正しい解決策に到達するためのより良いアルゴリズムはありますか? 私は正しい解決策にたどり着きましたか?