c# - 1/C# の BigInteger

Question

作りたい

BigInteger.ModPow(1/BigInteger, 2,5);

しかし、1/BigInteger常にを返します。0これにより、結果が0あまりにも大きくなります。c# のクラスを探しBigDecimalてみましたが、何も見つかりませんでした。なくてもこれを数える方法はありBigDecimalますか？

score 12 · Accepted Answer

1/aBigIntegers除算の小数部分が無視される整数除算を使用するため、|a|>1 の場合は 0 です。あなたがこれに期待している結果はわかりません。

分数ではなく、moduloの剰余乗法逆数にしたいと思います。この逆数は、互いに素である場合にのみ存在します。つまり、です。amamgcd(a, m) = 1

リンクされたウィキペディアのページには、剰余乗法逆数を計算するための 2 つの標準アルゴリズムがリストされています。

任意の係数で機能する拡張ユークリッドアルゴリズム
高速ですが、入力依存のランタイムがあります。

手元に C# コードはありませんが、ウィキペディアから疑似コードを移植するのは簡単です。
オイラーの定理の使用:
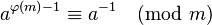
$i^{-1} = i^{φ(n)-1}$
これには、φ(m) の知識が必要です。つまり、m の素因数を知る必要があります。が素数の場合は一般的な選択肢mであり、単純にになると φ(m) = m-1 になり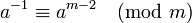 $a^{-1} = a^{p-2}$ ます。一定のランタイムが必要で、φ(m) がわかっている場合は、これが最適です。

C# では、これは次のようになります。BigInteger.ModPow(a, phiOfM-1, m)

score 1 · Accepted Answer

/選択した演算子の過負荷は次のとおりです。

public static BigInteger operator /(
        BigInteger dividend,
        BigInteger divisor
)

BigInteger.Division演算子を参照してください。結果がとの間0にある場合1（これは、あなたの場合のようになりそうdividendです1）、戻り値は整数であるため、ご覧のとおり、0が返されます。

この方法で何をしようとしていますModPowか？あなたはそれが「ツーポイントファイブ」ではなく、2と5の2つの議論であることに気づいてい2,5ますか？あなたの意図は「5を法とする平方を取る」ですか？

浮動小数点除算が必要な場合は、次を使用できます。

1.0 / (double)yourBigInt

へのキャストに注意してくださいdouble。yourBigIntこれにより、精度が低下し、大きすぎる場合は「アンダーフロー」がゼロになる可能性があります。

3 に答える 3