2

ハイブリッド ニューケインジアン フィリップス曲線は次のとおりです。

モデル

いくつかの操作の後、次の推定可能なモデルを取得します。

新しいモデル

ここで、πはインフレ率、xは産出ギャップ (= Hodrick-Prescott フィルターを使用した GDP の循環成分) の尺度です。モデルの説明変数πとxは観測可能です。

非線形最小二乗法を使用してこのモデルを推定する必要があります。ただし、このモデルは線形に見えます。nls()また、 Rで関数を使用しようとしても失敗しました。

また、非線形回帰に関する私の研究は、ロジスティック人口増加につながりましたが、特に開始値の導出に関しては、学んだことをこの演習に関連付ける方法を見つけることができません.

4

1 に答える 1

3

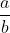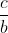関数で通常の最小二乗法 (OLS) を使用lm()して問題の式 (2) を推定すると、係数coef1およびcoef2が推定されcoef3ます。

一方、nls()関数で非線形最小二乗法を使用して方程式を推定すると、目的のパラメーターであるパラメーター 'a'、'b'、および 'c' の値が推定されます。

Rのnls()関数 (非線形最小二乗) には 2 つの重要なパラメーターがあります。最初にformulaパラメーター、次にstartパラメーターです。?nlsR で実行すると、いくつかの詳細が得られます。ただし、要点は、formulaパラメーターが推定したい非線形モデルの式を取り込むことです (たとえばy ~ a / (b + c*x)、「y」と「x」は変数で、「a」、「b」、および「c」はパラメーターです)。startパラメータは、R が反復プロセスで使用する、関心のあるパラメータの開始値を受け取ります (非線形最小二乗法は基本的に、パラメータの最適な値が得られるまで計算を繰り返すため) 。

手順は次のとおりです。

(i) パラメータ「a」、「b」および「c」の開始値を取得します

ここでは、lm()関数を使用して式 (2) の係数を推定しました。関数で使用するラグ変数を作成することから始めました。

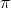円周率注意: 「y」は「 」を指します。

y_1 = c(NA, head(y, head(y, -1) # variable 'y' lagged  by one time period
y_2 = c(c(NA, NA), head(y, head(y, -2) # variable 'y' lagged by two time periods
x_1 = c(NA, head(x, head(x, -1) # variable 'x' lagged by one time period

したがって、方程式の係数を推定するために、次のコードが使用されました。

reg = lm(y ~ y_1 + y_2 + x_1, na.action = na.exclude) # it is important to tell R to exclude the missing values (NA) that we included as we constructed the lagged variables

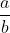coef1、coef2およびの推定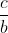coef3値が得られたので、次の方法で「a」、「b」、および「c」の値を計算できます。

B = 1 / reg$coefficients["y_1"] # Calculates the inverse of the coefficient on the variable 'y_1'

A = B * reg$coefficients["y_2"] # Multiplies 'b' by the coefficient on the variable 'y_2'

C = B * reg$coefficients["x_1"] # Multiplies 'b' by the coefficient on the variable 'x_1'

A、関数の開始値として使用されBますCnls()

(ii)nls()機能を使用する

nlreg = nls(y ~ (1/b)*y_1 - (a/b)*y_2 - (c/b)*x_1,
        start = list(a = A, b = B, c = C))

結果は次のコードで確認できます。

summary(nlreg)

洞察を提供してくれたBen Bolkerに感謝します:)

于 2013-02-24T17:38:10.260 に答える