私は赤黒木についてのwikiを読んでいました。
誰かが5番目の制限について詳しく説明できますか?
ノードは赤または黒のいずれかです。
根は黒です。
すべての葉(NIL)は黒です。(すべての葉は根と同じ色です。)
すべての赤いノードの両方の子は黒です。
特定のノードからその子孫リーフへのすべての単純なパスには、同じ数の黒いノードが含まれています。
挿入の最後のケース(wikiのケース5)が私たちに与えた後の例のRBTの状態を考えると、私はそれを理解するのに苦労しています:
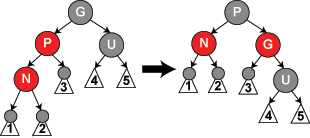
4と5には、1、2、3よりも1つ多いブラックノードがありませんか?