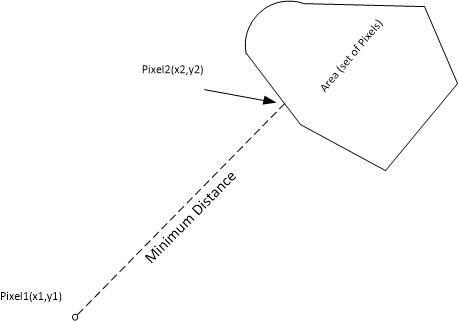
これが私のコードです。離散座標を使用した離散バージョンです。
ヒント: エリアの円周を見つけるために使用した方法は単純です。陸地からビーチをどのように知るかのようなものです。答え: ビーチは片側から海に覆われているので、私のグラフ マトリックスでは、NULL 参照は海、ポイントは陸地です!
クラスポイント:
class Point
{
public int x;
public int y;
public Point (int X, int Y)
{
this.x = X;
this.y = Y;
}
}
クラスエリア:
class Area
{
public ArrayList<Point> points;
public Area ()
{
p = new ArrayList<Point>();
}
}
離散距離ユーティリティ クラス:
class DiscreteDistance
{
public static int distance (Point a, Point b)
{
return Math.sqrt(Math.pow(b.x - a.x,2), Math.pow(b.y - a.y,2))
}
public static int distance (Point a, Area area)
{
ArrayList<Point> cir = circumference(area);
int d = null;
for (Point b : cir)
{
if (d == null || distance(a,b) < d)
{
d = distance(a,b);
}
}
return d;
}
ArrayList<Point> circumference (Area area)
{
int minX = 0;
int minY = 0;
int maxX = 0;
int maxY = 0;
for (Point p : area.points)
{
if (p.x < minX) minX = p.x;
if (p.x > maxX) maxX = p.x;
if (p.y < minY) minY = p.y;
if (p.y > maxY) maxY = p.y;
}
int w = maxX - minX +1;
int h = maxY - minY +1;
Point[][] graph = new Point[w][h];
for (Point p : area.points)
{
graph[p.x - minX][p.y - minY] = p;
}
ArrayList<Point> cir = new ArrayList<Point>();
for (int i=0; i<w; i++)
{
for (int j=0; j<h; j++)
{
if ((i > 0 && graph[i-1][j] == null)
|| (i < (w-1) && graph[i+1][j] == null)
|| (j > 0 && graph[i][j-1] == null)
|| (i < (h-1) && graph[i][j+1] == null))
{
cir.add(graph[i][j]);
}
}
}
return cir;
}
}