ある角度が別の角度から一定の角度内にあるかどうかを判断するためのアルゴリズムが必要です。
私の最初の考えはでしたが(a-x < b) && (a+x > b)、-179から180までの角度で動作する必要がある場合は失敗します。
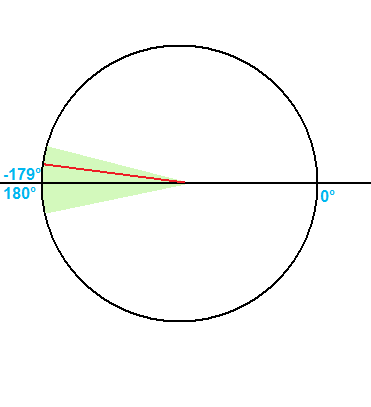
上の図では、角度が負の側と正の側の間のラップの間にある必要がある領域(緑)。角度(赤い線)がこの領域内にあるかどうかをどのように判断できますか?
ある角度が別の角度から一定の角度内にあるかどうかを判断するためのアルゴリズムが必要です。
私の最初の考えはでしたが(a-x < b) && (a+x > b)、-179から180までの角度で動作する必要がある場合は失敗します。

上の図では、角度が負の側と正の側の間のラップの間にある必要がある領域(緑)。角度(赤い線)がこの領域内にあるかどうかをどのように判断できますか?
この式を試してください:
360-(|a-b|)%360<x || (|a-b|)%360<x
または、PHPの場合:
<?php
$b = 10;
$angle1 = -179;
$angle2 = 180;
$diff = $angle1 - $angle2;
if(abs($diff % 360) <= $b || (360-abs($diff % 360))<=$b) {
echo "yes";
} else {
echo "no";
}
?>
ドット積を使用することもできます。
cos(a)*cos(b) + sin(a)*sin(b) >= cos(x)
マルセルが正しく指摘しているように、負の数のモジュロは潜在的に問題があります。また、355度と5度の違いは何ですか?350度になるかもしれませんが、おそらく10度が期待されています。次のことを前提としています。
0 <= diff <= 180;2*PIラジアンの場合は、 ;の代わりに360を使用します。-360 < x < 360。ここで、xは入力角度であり、入力:角度aおよびb。したがって、アルゴリズムは単純です。
0 <= x < 360;に正規化します。最初のステップでは、角度を目的の範囲に変換するには、次の2つの可能性があります。
x >= 0:通常= x%360x < 0:通常=(-x / 360 + 1)* 360 + x2つ目は、負の剰余演算の解釈の違いに関するあいまいさを取り除くように設計されています。したがって、x = -400の実際の例を示すには、次のようにします。
-x / 360 + 1
= -(-400) / 360 + 1
= 400 / 360 + 1
= 1 + 1
= 2
それから
normal = 2 * 360 + (-400)
= 320
したがって、入力10および-400の場合、通常の角度は10および320です。
次に、それらの間の最短角度を計算します。健全性チェックとして、これら2つの角度の合計は360でなければなりません。この場合、可能性は50と310です(描画するとこれが表示されます)。これらを解決するには:
normal1 = min(normal(a), normal(b))
normal2 = max(normal(a), normal(b))
angle1 = normal2 - normal1
angle2 = 360 + normal1 - normal2
したがって、この例では:
normal1 = min(320, 10) = 10
normal2 = max(320, 10) = 320
angle1 = normal2 - normal1 = 320 - 10 = 310
angle2 = 360 + normal1 - normal2 = 360 + 10 - 320 = 50
あなたは注意するでしょうnormal1 + normal2 = 360(そしてあなたが望むならこれが事実であることを証明することさえできます)。
最後に:
diff = min(normal1, normal2)
または私たちの場合は50。
半径 1 の場合、線の端点間の距離は 2sin((ab/2) です。比較にのみ関心があるため、2 を捨てて、sin(x/2) と sin((ab)/ 2). 三角関数がすべてのラッピングを処理します。
C++ 実装:
float diff = fabsf(angle1 - angle2);
bool isInRange = fmodf(diff, 360.0f) <= ANGLE_RANGE ||
360.0f - fmodf(diff, 360.0f) <= ANGLE_RANGE;