oracle - (a | b ) が a - (a & b) + b と等しいのはなぜですか?

Question

Oracle データベースで BITOR() を実行する方法を探していたところ、代わりに BITAND() を使用し、BITOR(a,b) を a + b - BITAND(a,b) に置き換えるという提案に出会いました。

私はそれを数回手でテストし、考えられるすべての2進数で機能するように見えることを確認しましたが、なぜこれが正しいのかを簡単に数学的に証明することはできません.
誰かが私を啓発できますか？

Answer 1

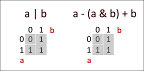
A & B は、A と B の両方でオンになっているビットのセットです。A - (A & B) は、A でのみオンになっているすべてのビットを残します。それに B を追加すると、すべてのビットが得られます。 AでオンまたはBでオンになっているもの。

A と B の単純な足し算は、どちらもビットが 1 であるキャリングのため機能しません。最初に A と B に共通するビットを削除することで、(A-(A&B)) には B と共通するビットがないことがわかります。

Answer 2

2つの2進数があると想像してください：aとb。そして、これらの数が同時に同じビットに1を持つことは決してないとしましょう。つまりa、あるビットに1がある場合b、対応するビットには常に0があります。また、他の方向でbは、あるビットに1がある場合、そのビットにはa常に0があります。例えば

a = 00100011
b = 11000100

これは、上記の条件の例でaあり、それbを満たしています。a | bこの場合、それがとまったく同じであることが簡単にわかりa + bます。

a | b = 11100111
a + b = 11100111

ここで、条件に違反する2つの数値を考えてみましょう。つまり、2つの数値には、いくつかの共通ビットに少なくとも1つの1があります。

a = 00100111
b = 11000100

この場合a | bと同じですか？a + bいいえ

a | b = 11100111
a + b = 11101011

なぜ違うのですか？+両方の数値に1があるビットを生成すると、いわゆるキャリーが生成されるため、これらは異なります。結果のビットは0であり、1は左側の次のビットにキャリーされます1 + 1 = 10。操作|にはキャリーがないので、1 | 1やはり1です。

a | bこれは、との違いはa + b、数値に共通ビットが少なくとも1つある場合にのみ発生することを意味します。共通ビットに1を含む2つの数値を合計すると、これらの共通ビットは「2回」加算されてキャリーを生成し、との間の類似性を台無しにa | bしa + bます。

今見てくださいa & b。何をa & b計算しますか？a & bすべてのビットに1があり、両方が1である数を生成しaますb。最新の例では

a =     00100111
b =     11000100
a & b = 00000100

上で見たように、これらはまさに。とはa + b異なるビットですa | b。の1はa & b、キャリーが発生するすべての位置を示します。

さて、そうするとき、私たちはすべての「問題のある」ビットa - (a & b)を効果的に削除a（減算）し、そのようなビットだけを削除します

a - (a & b) = 00100011

数字a - (a & b)でbあり、共通の1ビットはありません。つまり、加算a - (a & b)しbてキャリーに遭遇しない場合、それについて考えると、ちょうど行った場合と同じ結果になるはずです。a | b

a - (a & b) + b = 11100111

Answer 3

A&B = C ここで、C に設定されたままのビットは、A と B の両方に設定されたものです
。AC = D または BC = E は、これらの共通ビットだけを 0 に設定します。1-1=0 であるため、キャリー効果はありません。
D+B または E+A は A+B と似ていますが、前に A&B を減算したため、D または E で共通に設定されたすべてのビットがクリアされているため、キャリーはありません。

最終的な結果として、AA&B+B または BA&B+A は A|B と同等になります。

まだ混乱している場合は、真理値表を次に示します。

あ | ビ | または ビ | ＆A | ビ | - あ | ビ | +
---+---+---- ---+---+--- ---+---+--- ---+---+---
 0 | 0 | 0 0 | 0 | 0 0 | 0 | 0 0 | 0 | 0  
 0 | 1 | 1 0 | 1 | 0 0 | 1 | 0-1 0 | 1 | 1
 1 | 0 | 1 1 | 0 | 0 1 | 0 | 1 1 | 0 | 1  
 1 | 1 | 1 1 | 1 | 1 1 | 1 | 0 1 | 1 | 1+1

+ 操作と - 操作のキャリー行に注意してください。A-(A&B) セットのケースは A のビットと B の両方が A の 1 から 0 であり、B からそれらを追加すると、他のケースがあったため、それらを避けます。 A または B のいずれかで 1 でしたが、両方が 0 ではなかったので、OR 真理値表と A-(A&B)+B 真理値表は同一です。

注目するもう 1 つの方法は、A+B が一番下の行のキャリーを除いて A|B とほとんど同じであることを確認することです。A&B は一番下の行を分離し、AA&B は分離されたケースを + 表の 2 行上に移動し、(AA&B)+B は A|B と同等になります。

これを A+B-(A&B) に変更することはできますが、オーバーフローの可能性を恐れていましたが、それは正当化されなかったようです:

#include <stdio.h>
int main(){ unsigned int a=0xC0000000, b=0xA0000000;
printf("%x %x %x %x\n",a,   b,       a|b,       a&b);
printf("%x %x %x %x\n",a+b, a-(a&b), a-(a&b)+b, a+b-(a&b)); }

c0000000 a0000000 e0000000 80000000
60000000 40000000 e0000000 e0000000

編集：回答がある前にこれを書いた後、自宅の接続に約2時間のダウンタイムがあり、最終的に投稿することができましたが、後で適切に2回回答されたことに気付きました. 個人的には、真理値表を参照してビット単位の演算を行う方が好きなので、誰かの役に立つ場合に備えて残しておきます。

Answer 4