ルーレット選択関数の擬似コードを提供できる人はいますか? これをどのように実装しますか:
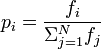
この数学表記の読み方がよくわかりません。私は確率や統計を取ったことがありません。
ルーレット選択関数の擬似コードを提供できる人はいますか? これをどのように実装しますか:
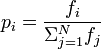
この数学表記の読み方がよくわかりません。私は確率や統計を取ったことがありません。
私がこれを自分で行ってから数年が経ちましたが、次の疑似コードはグーグルで簡単に見つかりました。
人口のすべてのメンバー
sum += この個体の適応度
終了
人口のすべてのメンバー
確率 = 確率の合計 + (適合度 / 合計)
確率の合計 += 確率
終了
新しい人口がいっぱいになるまでループ
これを2回行う
number = 0 から 1 の間のランダム
人口のすべてのメンバー
数値 > 確率で次の確率より小さい場合
あなたは選ばれました
終了
終わり
子孫を作る
エンドループ
詳細が必要な場合は、これの元のサイトをここで見つけることができます。
すでに多くの正しい解決策がありますが、このコードはより明確だと思います。
def select(fs):
p = random.uniform(0, sum(fs))
for i, f in enumerate(fs):
if p <= 0:
break
p -= f
return i
さらに、fsを累積すると、より効率的なソリューションを作成できます。
cfs = [sum(fs[:i+1]) for i in xrange(len(fs))]
def select(cfs):
return bisect.bisect_left(cfs, random.uniform(0, cfs[-1]))
これは高速であり、非常に簡潔なコードです。C ++のSTLには、使用している言語である場合に使用できる同様の二分アルゴリズムがあります。
投稿された疑似コードにはいくつかの不明確な要素が含まれており、純粋な選択を実行する代わりに子孫を生成するという複雑さが追加されています。その疑似コードの単純な python 実装を次に示します。
def roulette_select(population, fitnesses, num):
""" Roulette selection, implemented according to:
<http://stackoverflow.com/questions/177271/roulette
-selection-in-genetic-algorithms/177278#177278>
"""
total_fitness = float(sum(fitnesses))
rel_fitness = [f/total_fitness for f in fitnesses]
# Generate probability intervals for each individual
probs = [sum(rel_fitness[:i+1]) for i in range(len(rel_fitness))]
# Draw new population
new_population = []
for n in xrange(num):
r = rand()
for (i, individual) in enumerate(population):
if r <= probs[i]:
new_population.append(individual)
break
return new_population
これがCのコードです:
// Find the sum of fitnesses. The function fitness(i) should
//return the fitness value for member i**
float sumFitness = 0.0f;
for (int i=0; i < nmembers; i++)
sumFitness += fitness(i);
// Get a floating point number in the interval 0.0 ... sumFitness**
float randomNumber = (float(rand() % 10000) / 9999.0f) * sumFitness;
// Translate this number to the corresponding member**
int memberID=0;
float partialSum=0.0f;
while (randomNumber > partialSum)
{
partialSum += fitness(memberID);
memberID++;
}
**// We have just found the member of the population using the roulette algorithm**
**// It is stored in the "memberID" variable**
**// Repeat this procedure as many times to find random members of the population**
上記の回答から、次のことがわかりました。これは、回答自体よりも明確でした。
例を挙げると:
Random(sum) :: Random(12) 母集団を反復して、次のことを確認します: random < sum
乱数として 7 を選びましょう。
Index | Fitness | Sum | 7 < Sum
0 | 2 | 2 | false
1 | 3 | 5 | false
2 | 1 | 6 | false
3 | 4 | 10 | true
4 | 2 | 12 | ...
この例では、最も適合するもの (インデックス 3) が選択される割合が最も高くなります (33%)。乱数は 6->10 の範囲内に収まる必要があり、選択されます。
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
}
double rand = (((double)rand() / (double)RAND_MAX) * sum);
sum = 0;
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
if (rand < sum) {
//breed i
break;
}
}
これは、ルーレットを選択するために最近作成したコンパクトなJava実装であり、うまくいけば使用できます。
public static gene rouletteSelection()
{
float totalScore = 0;
float runningScore = 0;
for (gene g : genes)
{
totalScore += g.score;
}
float rnd = (float) (Math.random() * totalScore);
for (gene g : genes)
{
if ( rnd>=runningScore &&
rnd<=runningScore+g.score)
{
return g;
}
runningScore+=g.score;
}
return null;
}
MatLab でのルーレット盤の選択:
TotalFitness=sum(Fitness);
ProbSelection=zeros(PopLength,1);
CumProb=zeros(PopLength,1);
for i=1:PopLength
ProbSelection(i)=Fitness(i)/TotalFitness;
if i==1
CumProb(i)=ProbSelection(i);
else
CumProb(i)=CumProb(i-1)+ProbSelection(i);
end
end
SelectInd=rand(PopLength,1);
for i=1:PopLength
flag=0;
for j=1:PopLength
if(CumProb(j)<SelectInd(i) && CumProb(j+1)>=SelectInd(i))
SelectedPop(i,1:IndLength)=CurrentPop(j+1,1:IndLength);
flag=1;
break;
end
end
if(flag==0)
SelectedPop(i,1:IndLength)=CurrentPop(1,1:IndLength);
end
end
スタンフォード AI ラボの Thrun 教授も、Udacity の CS373 で、Python で高速な (er?) リサンプリング コードを提示しました。Google 検索結果は次のリンクにつながりました。
http://www.udacity-forums.com/cs373/questions/20194/fast-resampling-algorithm
お役に立てれば
Based on my research ,Here is another implementation in C# if there is a need for it:
//those with higher fitness get selected wit a large probability
//return-->individuals with highest fitness
private int RouletteSelection()
{
double randomFitness = m_random.NextDouble() * m_totalFitness;
int idx = -1;
int mid;
int first = 0;
int last = m_populationSize -1;
mid = (last - first)/2;
// ArrayList's BinarySearch is for exact values only
// so do this by hand.
while (idx == -1 && first <= last)
{
if (randomFitness < (double)m_fitnessTable[mid])
{
last = mid;
}
else if (randomFitness > (double)m_fitnessTable[mid])
{
first = mid;
}
mid = (first + last)/2;
// lies between i and i+1
if ((last - first) == 1)
idx = last;
}
return idx;
}
私はC#でバージョンを書きましたが、それが本当に正しいかどうかの確認を本当に探しています:
(roulette_selector は 0.0 から 1.0 の範囲の乱数です)
private Individual Select_Roulette(double sum_fitness)
{
Individual ret = new Individual();
bool loop = true;
while (loop)
{
//this will give us a double within the range 0.0 to total fitness
double slice = roulette_selector.NextDouble() * sum_fitness;
double curFitness = 0.0;
foreach (Individual ind in _generation)
{
curFitness += ind.Fitness;
if (curFitness >= slice)
{
loop = false;
ret = ind;
break;
}
}
}
return ret;
}