以下に示す関節ニューロンについて、それが発火する入力i1、i2、およびi3の値(0または1)を決定しようとしています(i0はバイアス重みの入力であり、常に-1になります)。
重みは
W0 = 1.5
W1 = -1
W2 = 1、およびW3=2。
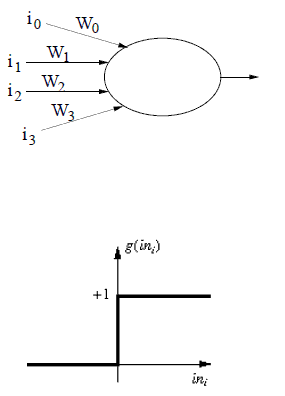
下の画像に示されている活性化関数を想定します。
私はいくつかの例を実行しましたが、それでも理論を完全に理解することはできませんので、あなたの答えを明確にしてください:(
どうもありがとう、
メアリーJ.
PS。下の画像:
以下に示す関節ニューロンについて、それが発火する入力i1、i2、およびi3の値(0または1)を決定しようとしています(i0はバイアス重みの入力であり、常に-1になります)。
重みは
W0 = 1.5
W1 = -1
W2 = 1、およびW3=2。
下の画像に示されている活性化関数を想定します。
私はいくつかの例を実行しましたが、それでも理論を完全に理解することはできませんので、あなたの答えを明確にしてください:(
どうもありがとう、
メアリーJ.
PS。下の画像:

基本的に、ニューロン出力には次の方程式がi1ありi2ますi3。
2*i3 + i2 - i1 - 1.5 >= 0
まず、正の加重値の最大値を見てみましょう。が 0 の場合i3、左辺で得られる最大値は -0.5 であるため、i3ゼロ以外の出力を得るには 1 にする必要があります。式は次のようになります。
i2 - i1 + 0.5 >= 0
次に、負の加重値を見てください。i1が 0 の場合、出力は常に 0 より大きくなりますi2。i1が 1 の場合i2、ゼロ以外の出力が存在するためには 1 である必要があります。
したがって、ゼロ以外の出力を作成するこれらの組み合わせがあります。
i1 i2 i3
0 0 1
0 1 1
1 1 1
この問題をより一般的な方法で解決するには、まず変数と固定パラメーターを確認します。
基本的に、入力重みベクトルw= [1.5, -1, 1, 2]と伝達関数が与えられ、次のように 入力ベクトルing(x) = (sign(x)+1)/2を見つけたいとします: w in' (行ベクトルと列ベクトルの積として) したがって:g(*) = +1
g( sum_over_i( w_i*in_i ) ) = 1 # product of vectors
g( w0*in0 + w1*in1 + w2*in2 + w3*in3 ) = 1 # roll out the sum
g( -1.5 - in1 + in2 + 2*in3 ) = 1 # replace the values of w and in
0.5*(sign(-1.5 - in1 + in2 + 2*in3)+1) = 1 # definition of g(x)
sign(-1.5 - in1 + in2 + 2*in3) = 1 # simplify
-1.5 - in1 + in2 + 2*in3 >= 0 # by def: [sign(x)=1 iff x>=0]
通常は導関数を計算してこの方程式を解きますが、 の入力は0またはの値しかとれないため、1単純にすべてのケース (2^nまたはの8ケースがある)を列挙できます。
in1 in2 in3 -1.5-in1+in2+2*in3
-----------------------------------
0 0 0 -1.5
0 0 1 0.5 *
0 1 0 -0.5
0 1 1 1.5 *
1 0 0 -2.5
1 0 1 -0.5
1 1 0 -1.5
1 1 1 0.5 *
したがって、上記の式が正であるinの値を取得します。
in * Wni1、2、3のどの組み合わせが肯定的な結果をもたらすかを合計して判断するだけの問題のようです。順列は 8 つしかないので、手で実行するだけです。
私はAIについて大まかな知識を持っていますが、私が知る限り、次のようになります。
入力の合計(Sigma i_n * W_n)は、発火しきい値より大きくなければなりません。2番目の画像は発火しきい値を示し、最初の画像は入力とその重みを示しています。
どの合計(バイアスを忘れないでください)が望ましいしきい値/強度になるかを理解する必要があります