24

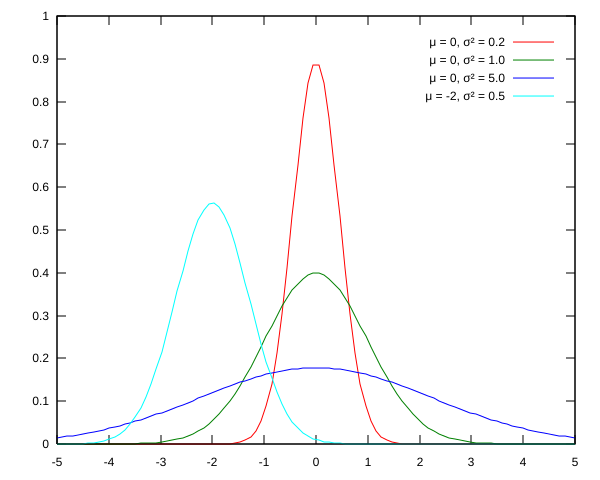
平均 0 とシグマ 1 の正規分布を生成するために、boost::normal_distribution を使用しようとしています。

次のコードは、一部の値が -1 と 1 を超えているか超えているため (そして、そうであってはならない) 機能しません。私が間違っていることを誰かが指摘できますか？

#include <boost/random.hpp>
#include <boost/random/normal_distribution.hpp>

int main()
{
  boost::mt19937 rng; // I don't seed it on purpouse (it's not relevant)

  boost::normal_distribution<> nd(0.0, 1.0);

  boost::variate_generator<boost::mt19937&, 
                           boost::normal_distribution<> > var_nor(rng, nd);

  int i = 0; for (; i < 10; ++i)
  {
    double d = var_nor();
    std::cout << d << std::endl;
  }
}

私のマシンでの結果は次のとおりです。

0.213436
-0.49558
1.57538
-1.0592
1.83927
1.88577
0.604675
-0.365983
-0.578264
-0.634376

ご覧のとおり、すべての値が -1 と 1 の間にあるわけではありません。

よろしくお願いします！

編集：これは、締め切りがあり、練習を行う前に理論の勉強を避けたときに起こることです.

4

2 に答える 2

29

次のコードは、一部の値が-1および1を超えているため、機能しません（また、そうではないはずです）。私が間違っていることを誰かが指摘できますか？

いいえ、これは正規分布の標準偏差（コンストラクター1の2番目のパラメーター）の誤解です。

正規分布は、おなじみのベルカーブです。その曲線は、値の分布を効果的に示しています。ベルカーブのピークに近い値は、遠くの値（分布の裾）よりも可能性が高くなります。

標準偏差は、値がどの程度広がっているかを示します。数値が小さいほど、平均値の周りに集中した値があります。数値が大きいほど、平均値の周りの集中度が低くなります。下の画像では、赤い曲線の分散（分散は標準偏差の2乗）が0.2であることがわかります。これを、平均は同じですが分散が1.0の緑色の曲線と比較してください。緑の曲線の値は、赤の曲線に比べてより広がっていることがわかります。紫色の曲線の分散は5.0で、値はさらに分散しています。

したがって、これは、値がに限定されない理由を説明しています[-1, 1]。ただし、値の68％が常に平均の1標準偏差内にあることは興味深い事実です。したがって、興味深いテストとして、平均が0で分散が1の正規分布から多数の値を抽出し、平均の1標準偏差内にある数を数えるプログラムを作成します。68％に近い数値を取得する必要があります（もう少し正確には68.2689492137％）。

代替テキスト

1：ブーストドキュメントから：

normal_distribution(RealType mean = 0, RealType sd = 1);

平均平均と標準偏差sdで正規分布を作成します。

于 2010-01-16T19:14:50.840 に答える
8

あなたは何も悪いことをしていません。正規分布の場合、sigma は範囲ではなく標準偏差を指定します。十分な数のサンプルを生成すると、[平均 - シグマ、平均 + シグマ] の範囲内にあるサンプルは約 68% のみで、約 95% が 2 シグマ内、99% 以上が 3 シグマ内にあることがわかります。

于 2010-01-16T18:57:12.440 に答える