8

次の問題を解決するために、適度なスペース要件で高速なアルゴリズムを見つけようとしています。

DAG の各頂点について、DAG の推移閉包の入次数と出次数の合計を求めます。

この DAG を考えると:

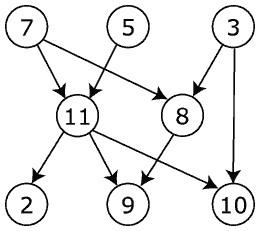
ウィキペディアの DAG

次の結果が期待されます。

Vertex #   Reacability Count  Reachable Vertices in closure
   7             5            (11, 8, 2, 9, 10)
   5             4            (11, 2, 9, 10)
   3             3            (8, 9, 10)
  11             5            (7, 5, 2, 9, 10)
   8             3            (7, 3, 9)
   2             3            (7, 5, 11)
   9             5            (7, 5, 11, 8, 3)
  10             4            (7, 5, 11, 3)

これは、推移閉包を実際に構築しなくても可能であるように思われます。この問題を正確に説明するものをネット上で見つけることができませんでした。これを行う方法についていくつかのアイデアがありますが、SO クラウドが何を思いつくかを見たかったのです。

4

5 に答える 5

2

正確な答えについては、KennyTM のアルゴリズムを打ち負かすのは難しいと思います。近似値で解決したい場合は、タンクのカウント方法 ( http://www.guardian.co.uk/world/2006/jul/20/secondworldwar.tvandradio ) が役立つ場合があります。

各頂点に範囲 [0, 1) の乱数を割り当てます。polygenelubricants のような線形時間動的プログラムを使用して、各頂点 v について、v から到達可能な minreach(v) の最小数を計算します。次に、v から到達可能な頂点の数を 1/minreach(v) - 1 として推定します。精度を高めるには、繰り返します。数回、各頂点で平均の中央値を取ります。

于 2010-03-06T17:59:09.103 に答える
1

ノードごとに、BFS または DFS を使用して到達可能性を見つけます。

逆方向にもう一度実行して、到達可能性を見つけます。

時間計算量: O(MN + N 2 )、空間計算量: O(M + N)。

于 2010-03-06T09:04:32.220 に答える
1

私はこの質問に対する実行可能な解決策を構築しました。私のソリューションは、トポロジカル ソートアルゴリズムの修正に基づいています。以下のアルゴリズムは、推移閉包での次数のみを計算します。出次数は、エッジを逆にして同じ方法で計算し、各頂点の 2 つのカウントを合計して、最終的な「到達可能カウント」を決定できます。

for each vertex V
   inCount[V] = inDegree(V)   // inDegree() is O(1)
   if inCount[V] == 0
      pending.addTail(V)

while pending not empty
   process(pending.removeHead())

function process(V)
   for each edge (V, V2)
      predecessors[V2].add(predecessors[V])   // probably O(|predecessors[V]|)
      predecessors[V2].add(V)
      inCount[V2] -= 1
      if inCount[V2] == 0
          pending.add(V2)
   count[V] = sizeof(predecessors[V])         // store final answer for V
   predecessors[V] = EMPTY                    // save some memory

集合操作が O(1) であると仮定すると、このアルゴリズムは O(|V| + |E|) で実行されます。ただし、set union 操作predecessors[V2].add(predecessors[V])によって多少悪化する可能性が高くなります。セット ユニオンに必要な追加の手順は、DAG の形状によって異なります。最悪のケースは O(|V|^2 + |E|) だと思います。私のテストでは、このアルゴリズムは、これまで試したどのアルゴリズムよりも優れたパフォーマンスを示しました。

さらに、完全に処理された頂点の先行セットを破棄することにより、このアルゴリズムは通常、ほとんどの代替方法よりも少ないメモリを使用します。ただし、上記のアルゴリズムの最悪の場合のメモリ消費量が推移閉包を構築する場合のメモリ消費量と一致することは事実ですが、ほとんどの DAG ではそうではありません。

于 2010-03-11T04:53:44.423 に答える
0

OMG それは間違っている! ごめん！

良い代替品が利用可能になるまで、これをそのままにしておきます。CW-ed ですので、可能であれば、自由に議論し、これについて拡張してください。

動的計画法を使用します。

for each vertex V
   count[V] = UNKNOWN
for each vertex V
   getCount(V)


function getCount(V)
   if count[V] == UNKNOWN
      count[V] = 0
      for each edge (V, V2)
        count[V] += getCount(V2) + 1          
   return count[V]

これはO(|V|+|E|)隣接リストを使用しています。推移閉包の出次数のみをカウントします。度数をカウントするには、getCountエッジを逆にして呼び出します。合計を取得するには、両方の呼び出しのカウントを合計します。

これがO(|V|+|E|)である理由を理解するには、次のことを考慮してください。各頂点Vは正確に何度も訪れます。11 + in-degree(V)回は直接 にV、1 回は各エッジに 1 回です(*, V)。その後の訪問でgetCount(V)は、 はメモ化count[V]された を単に返しますO(1)。

それを見る別の方法は、各エッジが何回たどられるかを数えることです: ちょうど 1 回です。

于 2010-03-06T07:23:30.623 に答える
0

すべての頂点のリストがあり、各頂点にはidそこから直接到達できる頂点のリストがあると仮定します。

次に、間接的に到達できる頂点を保持する別のフィールド (またはそれを表す方法) を追加できます。これを再帰的な深さ優先検索で行い、到達したそれぞれのノードのフィールドに結果をメモします。このためのデータ構造として、おそらく、重複を効率的に削除できるある種のツリーを使用するでしょう。

到達可能性は、逆リンクを追加することによって個別に実行できますが、到達可能性と同じパスで、現在到達しているノードを蓄積し、それらを到達したノードの対応するフィールドに追加することによって実行することもできます。

于 2010-03-06T11:44:13.330 に答える