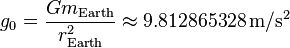algorithm - 重力ソート：これはプログラムで可能ですか？

Question

私は最近、ソートアルゴリズムでオブジェクト指向デザインを使用することを考えています。しかし、O（n）時間でソートを行うこのソートアルゴリズムを作成する際に、さらに近づくための適切な方法を見つけることができませんでした。

さて、これが私が一週間考えていたものです。入力データのセットがあります。各入力データに質量を割り当てます（入力データのタイプMassとタイプSphereを想定します。すべてのオブジェクトが、質量に比例した形状の完全な球形のオブジェクトであると仮定すると、最も重いオブジェクトが最初に地面に接触します）。すべての入力データを、地球からすべて同じ距離にある空間に配置します。そして、私はそれらを自由落下させます。重力の法則によれば、最も重いものが最初に地面にぶつかります。そして、それらがヒットした順序で、ソートされたデータが得られます。これはある意味おかしいですが、これまでに学んだOOを使ってこれが可能になるはずだと感じています

シナリオのような重力プルを使用するソート手法を作成することは本当に可能ですか、それとも私は愚かで狂っていますか？

編集：すべてのオブジェクトが同時に地面にぶつかることが判明したため、球形オブジェクトの概念を導入しました。

score 21 · Accepted Answer

OOP のアイデアの1 つは現実世界をモデル化することかもしれませんが、それは現実世界で何かがかかる時間とコンピューターでそれをシミュレートするのにかかる時間との間に直接的な対応があるという意味ではありません。

手順に必要な実際の手順を想像してください。

オブジェクトは、データセット内のすべてのアイテムに対して構築する必要があります。最新のほとんどのハードウェアでは、これだけで反復が必要になるため、戦略はせいぜいO(n) になります。
オブジェクトごとに、重力の影響をシミュレートする必要があります。繰り返しますが、これを実装する最も明白で簡単な方法は、反復することです。
プログラミングモデルで各オブジェクトが「地球」の表面に着陸する時間をキャプチャする必要があり、その結果として、実装固有のメカニズムを介して、対応するオブジェクトを順序付きリストに挿入する必要があります。

この問題を考慮すると、さらに複雑な問題が発生します。これを自問してみてください: これらのオブジェクトを開始するには、どのくらいの高さに配置する必要がありますか? 明らかに、最大のものが実際に落ちるのに十分な高さです。つまり、最大のオブジェクトの半径よりも地球から離れています。しかし、それがどのくらい離れているかをどのように知っていますか？最初にコレクション内の最大のオブジェクトを決定する必要があります。これもまた、（おそらく）反復が必要です。また、このシミュレーションをマルチスレッド化して、実際にオブジェクトの概念のリアルタイムの動作をシミュレートしようと試みることができると想像するかもしれません。落下; しかし、新しい衝突が検出されているのと同時に、コレクションにアイテムを追加しようとしていることに気付くでしょう (明らかにゼロ以外の時間がかかる操作です)。したがって、これによりスレッドの問題も発生します。

要するに、特別なハードウェアなしで OOP を使用するだけで、このアイデアを適切に実装する方法を想像するのは困難です。そうは言っても、それは本当に良い考えです。実際、これはBead Sortを思い出させます。このアルゴリズムは、あなたのアイデアと同じではありませんが、重力の非常に物理的な概念を利用し、驚くことではないが、特殊なハードウェアを必要とするソートソリューションでもあります。

score 9 · Accepted Answer

問題を言い直しました。重力効果の順序を計算すると、せいぜい、あなたが打ち負かそうとしているソートアルゴリズムのOが得られます。

score 7 · Accepted Answer

重力計算は実世界でのみ無料です。プログラムでは、それをモデル化する必要があります。最小の複雑さでさらにnになります

score 5 · Accepted Answer

アイデアは単純に見えるかもしれませんが、この場合の現実の世界とモデル化された世界の違いは、現実の世界ではすべてが並行して起こっているということです。説明したように重力ソートをモデル化するには、各オブジェクトを別のスレッドで考え、スレッドセーフな方法でそれらを終了順にリストに追加することから始める必要があります。現実的には、並べ替えのパフォーマンスに関しては、おそらく時間でクイック並べ替えを使用するか、落下率と同じ距離にあるためです。ただし、数式が質量に比例する場合は、それをすべてスキップして質量を並べ替えるだけです。

score 5 · Accepted Answer

汎用の並べ替えは、せいぜい O(n log n) であることが証明されています。これを改善するには、値を比較する方法以外に、データについて何かを知る必要があります。

値がすべて数値の場合、数値の上限と下限があると仮定すると、基数の並べ替えによって O(n) が得られます。このアプローチは、任意の数値を処理するように拡張できます。最終的に、コンピューター内のすべてのデータは数値を使用して表されます。たとえば、各パスで、1 文字を数字のようにソートすることで、文字列を基数ソートできます。

残念ながら、可変サイズのデータを処理するということは、基数ソートで可変数のパスを作成することを意味します。最終的には O(n log m) になります。ここで、m は最大値です (k ビットは、符号なしの場合は (2^k)-1 まで、符号付きの場合はその半分の値を与えるため)。たとえば、0 から m-1 までの整数を並べ替えると、実際には O(n log n) になります。

ある問題を別の問題に変換することは非常に優れたアプローチですが、場合によっては複雑さとオーバーヘッドがさらに増えるだけです。

score 3 · Accepted Answer

架空の「重力コンピューター」では、この種のソートを解くには O(1) が必要です。しかし、私たちが知っているような実際のコンピューターでは、横方向の思考は役に立ちません。

score 2 · Accepted Answer

実際には、スパゲッティソートと呼ばれる非常に有名なソートアルゴリズムがあります。これは、あなたのものと似ています。あなたはそれの多くの分析のいくつかをウェブ上でチェックすることができます。例：cstheory。

スパゲッティ

score 2 · Accepted Answer

地面に着くまでにかかるすべての時間を計算した後でも、それらの値を並べ替える必要があります。あなたは実際には何も得ていません、あなたはいくつかの余分な不必要な計算を実行した後に異なる数をソートしているだけです。

編集：おっと。物理学101を忘れました。もちろん、それらはすべて同時にヒットします。:)

このようなモデリングは、あるソート問題を別の問題に変換するだけです。あなたは何も得られません。

score 2 · Accepted Answer

うーん。重力ソート。

重力の特定のモデルを無視するのは間違っています。この考えが私たちをどこに連れて行くか見てみましょう.

物理的現実には 10^80 プロセッサがあります。

N 個のオブジェクトをソートするために N/2 個のプロセッサーがある場合、ソートの実際の下限は log(N) であることがわかっています。

利用可能な CPU コアが複数ある場合、複数のスレッドでマージソートを実行できない理由はありません。

score 2 · Accepted Answer

他の誰もが言及したすべての欠陥を無視すると、本質的にこれはO(n^2)アルゴリズムではなく、アルゴリズムに要約されO(n)ます。すべての「球体」を反復処理し、「最も重い」または「最大の」球体を見つけてから、それをリストにプッシュしてから、すすぎ、繰り返す必要があります。つまり、最初に地面に落ちたものを見つけるには、リスト全体を反復処理する必要があります。それが最後のものである場合はO(n)時間がかかり、2 番目のものはかかる可能性がO(n-1)あります...しかし、それより悪いのは、そもそも興味のある値でソートできたときに、役に立たない「時間」値を計算するためだけに、毎回一連の数学的演算を実行します。

score 1 · Accepted Answer

デビルスキーの答えから：

私はあなたの考えを少し適応させます。オブジェクトはありますが、重量は異なりませんが、速度は異なります。したがって、最初はすべてのオブジェクトが開始線と開始ショットで整列され、すべてのオブジェクトがそれぞれの速度で終了まで移動します。

十分にクリア：フィニッシュの最初のオブジェクトは、そこにあることを示す信号を発します。あなたは信号をキャッチし、それが誰であったかを結果用紙に書き込みます

私はそれをさらに単純化して、これらのオブジェクトはランダムな正の整数であると言います。また、ゼロに近づくにつれて昇順で並べ替えたいので、ゼロからの距離dは最初は整数自体に等しくなります。

シミュレーションが離散時間ステップ、つまりフレームで行われると仮定すると、すべてのフレームで、すべてのオブジェクトの新しい距離は次のようになります。d = d - vオブジェクトは、そのときにリストに追加されますd ≤ 0。これは、1つの減算と1つの条件付きです。オブジェクトごとに2つの個別のステップがあるため、計算はO（n）：線形のように見えます。

キャッチは、1フレームのみ線形です！終了するのに必要なフレーム数を掛けfます。シミュレーション自体はO（nf）：2次式です。

ただし、フレームの期間を引数として使用すると、反比例してtフレーム数に影響を与えることができます。f増やすtことで減らすこともできfますが、精度が犠牲になります。増やすほどt、2つのオブジェクトが同じ時間枠で終了する可能性が高くなります。したがって、そうでない場合でも、同等としてリストされます。したがって、精度を調整できるアルゴリズムを取得します（ほとんどの有限要素シミュレーションコンテキストでそうであるように）

これを適応+再帰アルゴリズムに変えることで、これをさらに洗練することができます。人間のコードでは、次のようになります。

function: FESort: arguments: OriginalList, Tolerance
  define an empty local list: ResultList

  while OriginalList has elements
    define an empty local list: FinishedList
    iterate through OriginalList
      decrement the distance of each object by Tolerance
      if distance is less than or equal to zero, move object from OriginalList to FinishedList

    check the number of elements in FinishedList
      when zero
        set Tolerance to double Tolerance
      when one
        append the only element in FinishedList to ResultList
      when more
        append the result of FESort with FinishedList and half Tolerance to ResultList
  
  return ResultList

誰かのために働く本当の同様の実装があるかどうか疑問に思います。

確かに興味深い主題:)

PS。上記の擬似コードは私の擬似コードの考え方です。もしあれば、もっと読みやすい、または適合した方法で自由に書き直してください。

score 1 · Accepted Answer

問題は次のように簡単にできると思います。球の底を異なる高さに配置して、同じ重力で落としたときに、最大のものが最初に地面にぶつかり、2番目に大きいものが次に地面に当たるようにします。これは基本的に使用するのと同じです。球ではなく線...この場合、heightOffTheGround=MAX_VALUE-質量と言うことができます。

また、時間の経過に伴う加速について心配する必要はありません...速度や現実的な物理学を気にしないので、すべての初速度xを与えて、そこから進むことができます。

問題は、基本的に問題を修正し、次のように解決したことです（擬似コード）。

int[] sortedArray; // empty
int[] unsortedArray; // full of stuff
int iVal = MAX_INT_VALUE;
while (true)
{
    foreach (currentArrayValue in sortedArray)
    {
        if (iVal = current array value
        {
            put it in my sortedArray
            remove the value from my unsortedArray
        }
    }
    if (unsortedArray is empty)
    {
        break;  // from while loop
    } 
    iVal--
}

問題は、物理エンジンを実行するには、時間単位ごとに反復する必要があることです。これは、O（1）になります...非常に大きな定数...システムが一定数のデルタ値を使用します実行します。欠点は、これらのデルタ値の大部分について、本質的に答えに近づくことができないことです。任意の反復で、すべての球/線/何でも移動する可能性が非常に高くなります...しかし、ヒットします。

あなたはただ言うことを試みることができます、まあ、多くの中間のステップをスキップして、1つがヒットするまでただ先にジャンプしましょう！しかし、それは、どれが最大であるかを知る必要があることを意味します...そして、ソートの問題に戻ります。

score 1 · Accepted Answer

いくつかの基準に基づいてオブジェクトをソートするコンピューターを構築する場合 (これを考えるのはまったくばかげているわけではありません)、複雑さの順序はオブジェクトの数とは関係なく、むしろ局所的な加速率と関係があると思います。重力による。地球でモデル化されていると仮定すると、複雑さは O(g ₀ ) になります。g ₀は次のとおりです。

$代替テキスト$

簡単な理由は、(n)最初に中心が揃っていれば、球状オブジェクトの数は関係ないということです。さらに、重力による加速度は、高さが増加するにつれて、高さ自体よりもはるかに大きな影響を与えます。たとえば、すべてのオブジェクトの高さを 10 倍にした場合、地面に衝突するまでの時間は 10 倍にはなりませんが、はるかに短くなります。加速度は実際には 2 つのオブジェクト間の距離に依存するため、これにはさまざまな無視できる近似が含まれますが、特定の値よりも全体像に関心があるため、無視できます。

それにもかかわらず、素晴らしいアイデア。

また、@Jeremy が投稿したコイン選別ビデオも気に入っています。そして最後に、オブジェクト指向性は、そのようなマシンを構築する上での私の関心事の中で最も重要ではありません. もっと考えてみると、このようなマシンを構築するための私の愚かな 2 セントは次のとおりです。

~~O 0 o O o~~

. . . . .
. . . . .
. . . . .
= = = = =

すべてのオブジェクトのサイズは、並べ替えの基準に比例して変化します。それらは最初、各球の中心を通る細い棒によって水平に保持されます。下部の=は、球体と衝突するとすぐにどこかに値 (オプションでその位置) を記録するように特別に設計されています。すべての球が衝突した後、記録された値に基づいてソートされた順序になります。

score 1 · Accepted Answer

私はアイデアが大好きです！賢いです。はい、他の人が言っていることは一般的に正しいですが、O(n log n) 境界は一般にソート問題の証明可能な下限ですが、その下限は比較ベースのモデルにのみ当てはまることに留意する必要があります。ここで提案しているのはまったく別のモデルであり、さらに検討する価値があります。

また、James と Matrix が指摘しているように、重いものは軽いものよりも速く移動するわけではありません。明らかに、重いオブジェクト (数) が実際に速く/遠くに (または遅く/少なく) 移動するようにモデルを適応させる必要があります。さらに）どうにかして数字を区別できるようにします（遠心分離機も思い浮かびます）。

もっと考える必要がありますが、あなたのアイデアは鋭いです!

(編集) Enrique の Phys2D のアイデアを見てみると、もっと理にかなっていると思います。

私が提案したいことの 1 つは、現時点では効率の側面を完全に無視することです。（私は知っています、私はそれが全体の目標だったことを知っています）。これは新しいモデルであり、まずアイデアとその実装の間のギャップを埋める必要があります。そうして初めて、このモデルにとって時間複雑度が何を意味するのかを理解することができます。

score 1 · Accepted Answer

適切なハードウェアがサポートされている必要があるのは間違いありません。そうでなければ、これは非常にクールなアイデアに思えます。誰かが IEEE の論文を発表して、このクレイジーな夢を視覚化してくれることを願っています。

score 1 · Accepted Answer

数週間前、私は同じことを考えていました。

私はPhys2Dを使用することを考えましたそれを実装するためのライブラリ。実用的ではないかもしれませんが、ただの楽しみです。オブジェクトに負の重みを割り当てて、負の数を表すこともできます。phys2d ライブラリを使用すると、負の重量を持つオブジェクトが屋根に移動し、正の重量を持つオブジェクトが落下するように重力を定義できます。次に、床と屋根の間の距離が同じになるように、すべてのオブジェクトを床と屋根の中間に配置します。結果の配列 r[] が length=number of objects であるとします。次に、オブジェクトが屋根に触れるたびに、配列 r[0] の先頭に追加し、カウンターをインクリメントします。次にオブジェクトが屋根に触れると、オブジェクトが床に到達するたびに r[1] に追加します。配列 r[r.length-1] の最後に追加し、次回は r[r.length-2] に追加します。最後に、そうしなかったオブジェクト

これは効率的ではありませんが、アイデアを実装するのに役立ちます。

score 1 · Accepted Answer

あなたの考えを少し修正します。オブジェクトはありますが、重さではなく速度が異なります。そのため、最初はすべてのオブジェクトがスタートラインに配置され、スタートショットではすべてのオブジェクトがそれぞれの速度でゴールまで移動します。

十分に明確です。finish の最初のオブジェクトは、そこにあることを示す信号を発します。あなたは合図をキャッチし、それが誰であったかを結果用紙に書きます。

さて、それをシミュレートしたいと思うでしょう。

フィールドの長さをとしますL=1。ステップサイズ∆tを使用すると、各Nオブジェクトが一度にの長さ移動しますvᵢ∙∆t。つまり、各オブジェクトsᵢ = L / (vᵢ∙∆t)には、仕上げに到達する前にステップが必要です。

ポイントは、速度が非常に近い 2 つのオブジェクトを区別するために、すべてのオブジェクトに異なるステップサイズを設定する必要があるということです。

最良の場合、これはオブジェクト 1 が 1 ステップで終了し、オブジェクト 2 が 2 ステップで終了することを意味します。したがって、総ステップ数はですS = 1 + 2 + … + N = N∙(N + 1)/2。これは順当N∙Nです。

それが最良のケースではなく、速度が互いに等しく接近していない場合は、ステップサイズを小さくして、実際には何度も反復する必要があります。

score 0 · Accepted Answer

言及/参照するのはいいことだと思います: P 対 NP と NP 問題を効率的に解決する自然の能力との関係は何ですか? 並べ替えはですO(nlog(n))。なぜ NP 困難な問題を解決しようとしないのですか?
物理法則により、物体は重力定数に比例して落下し、質量は無視できます。
物理プロセスのシミュレーションは、実際の時間の複雑さに影響を与える可能性があります。

algorithm - 重力ソート：これはプログラムで可能ですか？

19 に答える 19

Related

Reference