2

任意の 3 つのセット A、B、C について: B と C の結合 (編集: 交差) の一部である A の要素があるかどうかを (プログラムで) 判断する方法はありますか?

例:
A: 3 より大きいすべての数値
B: 7 未満のすべての
数値 C: 5 に等しいすべての数値

この場合、セット A には要素があり、数字 5 で適合します。仕様として実装していますので、この数値範囲は一例です。A、B、Cは何でも構いません。

4

3 に答える 3

5

編集： ありがとうニキ！

場合に役立ちますB.Count <= C.Count <= A.Count。

D = GetCommonElements(B,C);
if( D.Count>0 && GetCommonElements(D,A).Count >0)
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

SET GetCommonElements(X,Y)
{
    common = {}
    for x in X:
       if Y.Contains(x):
         common.Add(x);
    return common;
}

効率的な集合交差アルゴリズムを見てください。

集合の分配法則を使用できます

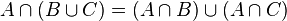
代替テキスト

if(HasCommonElements(A,B) || HasCommonElements(A,C))
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}


bool HasCommonElements(X,Y)
{
    // if at least one common element is found return true(immediately)

    return false
}
于 2010-04-13T19:47:06.233 に答える
1

私があなたの質問を正しく理解していれば、プログラムで 3 セットの交点を計算したいと思いますよね? B と C の交点に存在する A の要素があるかどうかを確認したい、つまり、A、B、C の交点が空でないかどうかを知りたい。

多くの言語ではコンテナと交差アルゴリズムが設定されているため、それらをそのまま使用できるはずです。OCaml での例:

module Int = struct
    type t = int
    let compare i j = if i<j then -1 else if i=j then 0 else 1
end;;

module IntSet = Set.Make(Int);;

let a = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [4;5;6;7;8;9;10];;
let b = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [0;1;2;3;4;5;6];;
let c = IntSet.add 5 IntSet.empty;;

let aIbIc = IntSet.inter (IntSet.inter b c) a;;
IntSet.is_empty aIbIc;;

ab と c の交点が空でない (5 を含む) ため、これは false を出力します。もちろん、これはセットの要素が比較可能であるという事実に依存しています (例では、関数 compare が Int モジュールでこのプロパティを定義しています)。

あるいは、C++ の場合:

#include<iostream>
#include<set>
#include<algorithm>
#include<iterator>

int main()
{
    std::set<int> A, B, C;

    for(int i=10; i>3; --i)
        A.insert(i);
    for(int i=0; i<7; ++i)
        B.insert(i);
    C.insert(5);

    std::set<int> ABC, BC;
    std::set_intersection(B.begin(), B.end(), C.begin(), C.end(), std::inserter(BC, BC.begin()));
    std::set_intersection(BC.begin(), BC.end(), A.begin(), A.end(), std::inserter(ABC, ABC.begin()));

    for(std::set<int>::iterator i = ABC.begin(); i!=ABC.end(); ++i)
    {
        std::cout << *i << " ";
    }
    std::cout << std::endl;

    return 0;
}
于 2010-04-13T23:13:31.620 に答える
0

この質問はさらに明確にする必要があります。まず、範囲で指定された記号セットを使用しますか? 次に、それは 1 回限りの質問ですか、それとも何らかの形で繰り返される予定ですか (そうであれば、質問の安定した部分は何ですか?)。

範囲を操作する場合は、これらを二分木で表現し、これらの構造で和集合と交差操作を定義できます。ツリーを構築するには O(n log n) が必要であり、結果を見つけるには O(log n) が必要です。これは、ツリー セットだけでは効果がありませんが、範囲の任意の組み合わせを効率的にサポートする柔軟性があります (それが「何でもかまいません」と考えた場合)。

一方、要素の任意のセットを意味する場合、唯一のオプションは要素を列挙することです。この場合、セット B と C に B+ ツリーを構築するのにも O(n log n) の時間が必要ですが、ここで n は要素の数であり、最初のケースでは n は範囲の数です。後者は数桁大きくなる可能性があり、もちろん、有限数の要素しか表すことができません。

于 2010-04-14T17:59:24.743 に答える