下のプロットの信頼区間の外側にあるデータポイントを、帯域内のデータポイントとは異なる色にする必要があります。データポイントが信頼区間内にあるかどうかを記録するために、データセットに別の列を追加する必要がありますか?例を挙げていただけますか?
データセットの例:
## Dataset from http://www.apsnet.org/education/advancedplantpath/topics/RModules/doc1/04_Linear_regression.html
## Disease severity as a function of temperature
# Response variable, disease severity
diseasesev<-c(1.9,3.1,3.3,4.8,5.3,6.1,6.4,7.6,9.8,12.4)
# Predictor variable, (Centigrade)
temperature<-c(2,1,5,5,20,20,23,10,30,25)
## For convenience, the data may be formatted into a dataframe
severity <- as.data.frame(cbind(diseasesev,temperature))
## Fit a linear model for the data and summarize the output from function lm()
severity.lm <- lm(diseasesev~temperature,data=severity)
# Take a look at the data
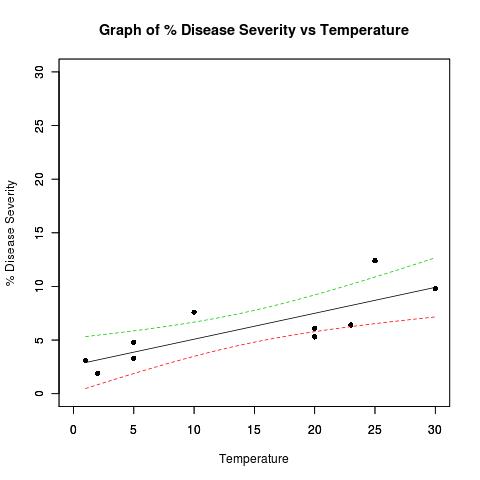
plot(
diseasesev~temperature,
data=severity,
xlab="Temperature",
ylab="% Disease Severity",
pch=16,
pty="s",
xlim=c(0,30),
ylim=c(0,30)
)
title(main="Graph of % Disease Severity vs Temperature")
par(new=TRUE) # don't start a new plot
## Get datapoints predicted by best fit line and confidence bands
## at every 0.01 interval
xRange=data.frame(temperature=seq(min(temperature),max(temperature),0.01))
pred4plot <- predict(
lm(diseasesev~temperature),
xRange,
level=0.95,
interval="confidence"
)
## Plot lines derrived from best fit line and confidence band datapoints
matplot(
xRange,
pred4plot,
lty=c(1,2,2), #vector of line types and widths
type="l", #type of plot for each column of y
xlim=c(0,30),
ylim=c(0,30),
xlab="",
ylab=""
)