3

私の同僚が、オンラインのジャッジ Web サイトから、小さな町の避難計画の問題をグラフで解くという演習を提案してくれました。

私は答えを必要としません（また、私はそれを望んでいません）、私はこの種の問題に少し慣れていないので、それを解決するための最良のアプローチについてのアドバイスが必要です。

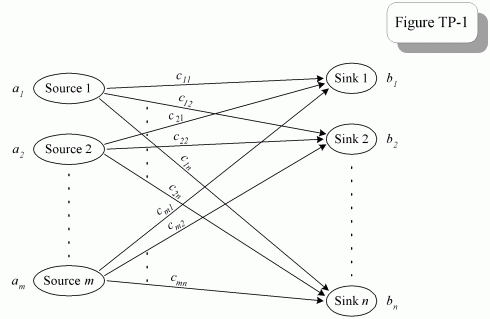
問題は、核攻撃の場合の労働者と放射性降下物シェルターのある町の建物で構成されています。各建物の労働者を 1 つまたは複数の放射性降下物シェルターに割り当てるアルゴリズムを構築する必要がありますが、一部のシェルターが過密になりすぎず、他のシェルターはほとんど空のままになるようにする必要があります (そうでない場合は、労働者を最寄りのシェルターに移動させるだけです)。 .

問題はこれです：http://acm.timus.ru/problem.aspx?space=1&num=1237

オフラインの場合は、Google キャッシュ バージョンを参照してください。 kotov+避難+問題&cd=1&hl=pt-PT&ct=clnk&gl=pt

私がこれまでに行ったことは、各建物が最も近い避難所を取得し、その建物から避難所の容量に等しい数の労働者を移動させることです。その後、次の建物に移動します。しかし、時には労働者の数がシェルターの収容能力よりも多い場合があります。その場合、すべての建物を繰り返し処理した後、すべての建物に労働者が0人になるまで同じアルゴリズムを繰り返し適用します。問題は、これが最善の方法ではないことです。それを解決します。

どんなヒントでも大歓迎です。答えを求めているような気がしないでください。それを解決するための正しい方向へのアドバイスが欲しいだけです。

前もって感謝します。

4

2 に答える 2

3

これは、線形計画法を使用して (明らかに) 解決できる転載問題とまったく同じように見えます。(どうやら、これは整数線形計画法 (Integer Linear Programming) のインスタンスのように見えるため)。

サイトから:

輸送の問題が発生する標準的なシナリオは、特定の都市のセットを接続する高速道路のネットワークを介して製品のユニットを送信するシナリオです。各都市は、ユニットがそこから出荷されるという点で「ソース」と見なされるか、ユニットがそこで要求されるという点で「シンク」と見なされます。各ソースには特定の供給があり、各シンクには特定の需要があり、ソースとシンクのペアを接続する各ハイウェイには、出荷単位あたりの特定の輸送コストがあります。これは、下の図 TP-1 に示すように、ネットワークの形で視覚化できます。

積み替え問題の図

このようなネットワークが与えられた場合、関心のある問題は、需要と供給の制約を受けて、出荷の総コストを最小限に抑える最適な輸送スキームを決定することです。

それが役立つことを願っています。

于 2010-05-19T16:42:56.833 に答える
2

これは、標準の最小コスト最大フロー問題のように見えます。200 個までの頂点を持つ 2 部グラフは、時間内に簡単に実行できるはずです。

頂点制約を作成するには (各ノードは k 人しか処理できません)、2 番目のグラフ G_1 を作成し、各 v_i に追加の頂点 u_i を追加する必要があります。 k+1 の場合、コストは 0 です。したがって、基本的に、元のグラフ G にエッジ (a,b) がある場合、G_1 には、これらのエッジのそれぞれに対してエッジ (u_a,v_b) が存在します。実際には、頂点ごとにフローを k に制限する頂点の 2 番目のレイヤーを作成しています。

于 2010-05-19T15:23:44.573 に答える