2

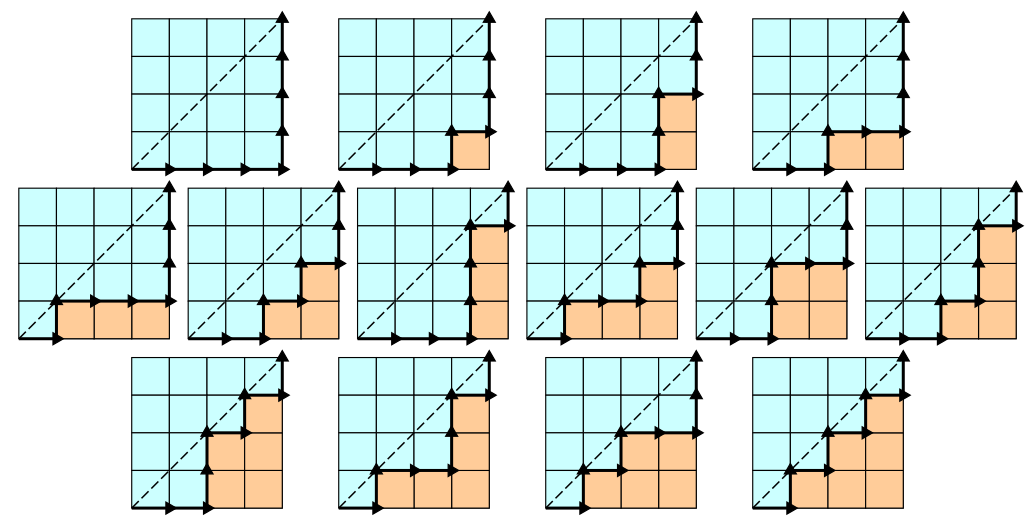
対角線の上を通過しない、n × n の正方形セル ( pic )

を持つグリッドのエッジに沿った単調格子パスのカタロニア語数を計算する再帰関数を作成するように依頼されました ( pic )。ループ、再帰呼び出しのみ...これは私がしたことです:

public long C(int n) {
    if (n == 1)
        return 0;
    return C(n, 0, 0);
}

private long C(int n, int i, int j) {

    // CAN MOVE UP & RIGHT
    if (j - i > 0 && j + 1 <= n)
        return paths(n, i + 1, j) + paths(n, i, j + 1);
    // CAN MOVE UP
    else if (j - i > 0)
        return paths(n, i + 1, j);
    // CAN MOVE RIGHT
    else if (j + 1 <= n)
        return paths(n, i, j + 1);
    // CAN'T MOVE
    else
        return 1;
}

このコードが最適かどうかはわかりませんが、機能します... この関数をメモ化関数に変換したいと考えています。しかし、それが機能をより効率的にする方法と理由を理解できません。メモ化されたフィボナッチの方が効率的である理由は理解できますが、ここでは常にパスの最後に到達してから 1 または 0 を返さなければならないので、配列内に 1 / 0 を格納するとどうなりますか?

あらゆる種類の助けをありがとう

4

2 に答える 2

3

しかし、[...]なぜそれが機能をより効率的にするのか理解できません。

画像を見て、画像に 1 から番号を付け、(x,y)座標を(0,0)左下隅にすると、画像 2、3、4、5、6、7、8、10、12 がすべて の点を通過していることがわかります。(3,1).

からのパス(3,1):

  • (3,1) → (4,1) ↑ (4,2) ↑ (4,3) ↑ (4,4)
    • 写真2、4、5
  • (3,1) ↑ (3,2) → (4,2) ↑ (4,3) ↑ (4,4)
    • 写真3、6、8
  • (3,1) ↑ (3,2) ↑ (3,3) → (4,3) ↑ (4,4)
    • 写真7、10、12

ご覧のとおり、同じ道を複数回 (3 回) 歩いています。最後まで3 つのパスがあるという事実をキャッシュ (メモ化) できれば(3,1)、時間を節約できます。

グリッドが大きくなるにつれて、時間の節約は大きくなります。

カタロニア語の数字 4x4 グリッドの例

したがって、最初にポイントに到達するときは、すでに行っているように再帰を使用して結果を計算し、そのポイントの数値を保存し、再びポイントに到達するときにキャッシュされた値を使用するだけです:

public static long paths(int n) {
    if (n == 1)
        return 0;
    return paths(n, 0, 0, new long[n][n]);
}
private static long paths(int n, int y, int x, long[][] cache) {
    long result = cache[y][x];
    if (result == 0) {
        if (y < x && x < n) // CAN MOVE UP & RIGHT
            result = paths(n, y + 1, x, cache) + paths(n, y, x + 1, cache);
        else if (y < x) // CAN MOVE UP
            result = paths(n, y + 1, x, cache);
        else if (x < n) // CAN MOVE RIGHT
            result = paths(n, y, x + 1, cache);
        else // CAN'T MOVE
            result = 1;
        cache[y][x] = result;
    }
    return result;
}
于 2015-12-12T20:05:45.757 に答える
1

メモ化が何であるかを知っているようです。基本的には、到達した値を格納するテーブルを作成するmemoだけなので、再帰で再度計算する必要はありません。fibonacci(5)なぜを見つけるために再帰に入る必要がないのfibonacci(3)と似たようなものです。私はあなたがそれを得る願っています。これが同じ精神でメモ化されたコードです。Andrea の質問には、わかりやすいビジュアルが用意されています。fibonacci(6)

long[][]memo;  //Memo table

public long C(int n)
{
    if (n == 1)
        return 0;

    memo=new int[n+1][n+1]; //Increase to n+1 and won't crash!

    for(int i=0;i<=n;i++)
        for(int j=0;j<=n;j++)
            memo[j][i]=-1;

    return C(n, 0, 0, memo);
}

private long C(int n, int i, int j, it) {

    // CAN MOVE UP & RIGHT
    if (j - i > 0 && j + 1 <= n)
    {
        if(memo[i+1][j]==-1)
            memo[i+1][j]=paths(n, i + 1, j);

        if(memo[i][j+1]==-1)
            memo[i][j+1]=paths(n, i, j + 1);

        return memo[i+1][j]+memo[i][j+1];
    }
    // CAN MOVE UP
    else if (j - i > 0)
    {
        if(memo[i+1][j]==-1)
            memo[i+1][j]=paths(n, i + 1, j);
        return memo[i+1][j];
    }
    // CAN MOVE RIGHT
    else if (j + 1 <= n)
    {
        if(memo[i][j+1]==-1)
            memo[i][j+1]=paths(n, i, j + 1);
        return memo[i][j+1];
    }
    // CAN'T MOVE
    else
        return 1;
}
于 2015-12-12T20:02:26.333 に答える