下の画像のようなグリッド上で許容される動きを把握するための適切な方法を誰かが提案できますか?
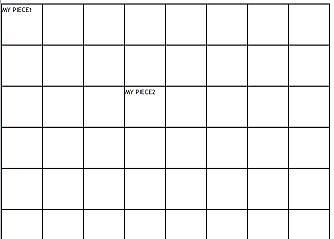
piece1が位置a1にあり、piece2が位置c3にあるとすると、piece1が(たとえば)3つの正方形を移動でき、piece2が2を移動できる場合、どのグリッドの正方形が許容される移動であるかをどのように判断できますか?
テキストベースのMUDSの開発に長い時間を費やしてきたようですが、最も単純な状況でも、潜在的な動きを視覚化する方法に脳を次のステップに進めることができません。
重要な場合、私はこれをjavascriptで実行しようとしていますが、正直に言うと、ここでの私の失敗は、言語理解の失敗ではなく、適切に概念化することの失敗だと思います。
更新-以下の回答が投稿された後に書かれた最初のコードを追加します。私と同じような状況の人にとって、コードを見るのは役に立つかもしれないと思いました
それはずさんで、これまでボードに配置された1つのアイテムに対してのみ機能しますが、少なくともこのcheck_allowable_moves()関数はこの最初の実行に対して機能します。数値のx軸とy軸を使用するだけでなく、なぜ私がこれらの奇妙な英数字オブジェクトを作成しているのか疑問に思っている人のために、HTMLのIDは数字で始めることができないためです。実際、IDを開始するために数字を使用できるふりをすることは、私が得た素晴らしい答えによって記述された機能と概念を理解するのに大いに役立ちました。
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" xml:lang="en" lang="en">
<head>
<meta http-equiv="Content-Type" content="application/xhtml+xml;utf-8"/>
<title>Test page</title>
<style>
#chessboard { clear: both; border:solid 1px black; height: 656px;
width:656px; /*width = 8*40 + 16 for border*/ }
#chessboard .row { overflow: auto; clear: both; }
#chessboard .row span { display: block; height: 80px;
width: 80px; float: left;
border:solid 1px black; }
.allowable { background: blue; }
</style>
<script type="text/javascript" src="http://www.google.com/jsapi"></script>
<script type="text/javascript">
google.load("jquery", "1.2.6");
google.load("jqueryui", "1.5.3");
</script>
<script type="text/javascript">
$(document).ready(function() {
(function() {
var global = this;
global.Map = function(container) {
function render_board() {
var max_rows = 8;
var cols = new Array('a','b', 'c', 'd', 'e', 'f', 'g', 'h');
var jqMap = $('<div />');
jqMap.attr('id', 'chessboard');
var x=0;
for(x; x<max_rows; x++) {
var jqRow = $('<span />');
jqRow.addClass('row');
var i=0;
for(i; i<cols.length; i++) {
var jqCol = $('<span />');
jqCol.attr('id', cols[i]+(x+1));
jqCol.addClass(cols[i]);
jqRow.append(jqCol);
}
jqMap.append(jqRow);
}
$('#'+container).append(jqMap);
}
function add_piece(where, id) {
var jqPiece = $('<div>MY PIECE'+id+'</div>');
var jqWhere = $('#'+where);
jqPiece.attr('id', 'piece-'+id);
jqPiece.addClass('army');
jqPiece.draggable({cursor: 'move',
grid:[82, 82],
containment: '#chessboard',
revert: 'invalid',
stop: function(ev, ui) {
//console.log(ev.target.id);
}
});
jqWhere.append(jqPiece);
check_allowable_moves(where);
}
function check_allowable_moves(location) {
var x_axis = { 'a':1,'b':2, 'c':3, 'd':4, 'e':5, 'f':6, 'g':7, 'h':8 };
var x_axis_alpha = { 1:'a',2:'b', 3:'c', 4:'d', 5:'e', 6:'f', 7:'g', 8:'h' };
$('.allowable').droppable("destroy");
$('.allowable').removeClass('allowable');
//get the x,y values of the piece just placed
var x = parseInt(x_axis[location[0]], 10);
var y = parseInt(location[1], 10);
var x_min = x-2;
var y_min = y-2;
for(x_min; x_min<=x+2; x_min++) {
for(y_min; y_min<=y+2; y_min++) {
var jqCell = $('#'+x_axis_alpha[x_min]+y_min)
jqCell.addClass('allowable');
jqCell.droppable({ accept: '.army',
drop: function(ev, ui) {
//console.log(ev, ui, $(this));
//handle_drop(ev, ui, $(this));
check_allowable_moves($(this).attr('id'));
}
});
}
y_min = parseFloat(y)-2;
}
}
render_board();
add_piece('d5', '2');
}
})();
var map = new Map('content');
});
</script>
</head>
<body id="debug">
<div id="page">
<div id="content"> </div>
</div><!-- end page -->
</body>
</html>