22

Stack Overflowポッドキャスト＃36（https://blog.stackoverflow.com/2009/01/podcast-36/）で、この意見が表明されました。ステートマシンのセットアップがいかに簡単かを理解したら、次のようになります。正規表現を不適切に使用しようとしないでください。

私はたくさんの検索をしました。いくつかの学術論文やその他の複雑な例を見つけましたが、このプロセスを理解するのに役立つ簡単な例を見つけたいと思います。私は正規表現をたくさん使用していますが、「不適切な」正規表現を二度と使用しないようにしたいと思います。

4

6 に答える 6

27

もちろん、REがどのように機能するかを真に理解するには、より複雑な例が必要になります。次のREを検討してください。

^[A-Za-z][A-Za-z0-9_]*$

これは一般的な識別子です（アルファで始まる必要があり、その後に英数字とアンスコア文字をいくつでも含めることができます。これには何も含まれません）。次の擬似コードは、これを有限状態マシンで実行する方法を示しています。

state = FIRSTCHAR
for char in all_chars_in(string):
    if state == FIRSTCHAR:
            if char is not in the set "A-Z" or "a-z":
                error "Invalid first character"
            state = SUBSEQUENTCHARS
            next char
    if state == SUBSEQUENTCHARS:
            if char is not in the set "A-Z" or "a-z" or "0-9" or "_":
                error "Invalid subsequent character"
            state = SUBSEQUENTCHARS
            next char

さて、私が言ったように、これは非常に単純な例です。貪欲/非貪欲な一致、バックトラック、行内での一致（行全体ではなく）、およびRE構文で簡単に処理できるステートマシンの他のより難解な機能の実行方法については説明していません。

そのため、REは非常に強力です。ワンライナーREが実行できることを実行するために必要な実際の有限状態マシンコードは、通常、非常に長く複雑です。

あなたができる最善のことは、特定の単純な言語のlex / yacc（または同等の）コードのコピーを取得して、それが生成するコードを確認することです。それはきれいではありませんが（人間が読むことを想定していないので、そうである必要はありません。彼らはlex / yaccコードを見ることになっています）、それらがどのように機能するかについてより良いアイデアを与えるかもしれません。

于 2009-02-08T02:36:43.613 に答える
26

これを見て、python のあまり知られていない re.DEBUG フラグを任意のパターンで使用するのに役立つかなり便利な方法:

>>> re.compile(r'<([A-Z][A-Z0-9]*)\b[^>]*>(.*?)</\1>', re.DEBUG)
literal 60
subpattern 1
  in
    range (65, 90)
  max_repeat 0 65535
    in
      range (65, 90)
      range (48, 57)
at at_boundary
max_repeat 0 65535
  not_literal 62
literal 62
subpattern 2
  min_repeat 0 65535
    any None
literal 60
literal 47
groupref 1
literal 62

'literal' と 'range' の後の数字は、一致するはずの ASCII 文字の整数値を参照します。

于 2009-02-08T03:01:01.723 に答える
20

その場であなた自身を作ろう！

http://osteele.com/tools/reanimator/???

有限状態機械

これは、正規表現を FSM として視覚化する非常にうまくまとめられたツールです。実際の正規表現エンジンに見られる構文の一部はサポートされていませんが、何が起こっているのかを正確に理解するには十分です。

于 2009-02-08T02:46:18.227 に答える
4

「状態と遷移条件を選択するにはどうすればよいですか?」または「Foo で抽象状態マシンを実装するにはどうすればよいですか?」という質問です。

状態と遷移条件を選択するにはどうすればよいですか?

私は通常、かなり単純な問題に FSM を使用し、直感的に選択します。正規表現に関する別の質問への回答では、解析の問題をどちらかInsideまたはoutsideタグのペアのいずれかとして見て、そこからの遷移を書き出しました (実装をクリーンに保つために開始状態と終了状態を使用)。

抽象状態マシンを Foo に実装するにはどうすればよいですか?

実装言語がcのswitchステートメントのような構造をサポートしている場合は、現在の状態に切り替えて入力を処理し、次にどのアクションやトランジションが実行されるかを確認します。

のような構造がないswitch場合、または何らかの形で不足している場合は、if分岐のスタイルを設定します。うーん。

リンクした例を 1 か所にcまとめると、次のようになります。

token_t token;
state_t state=BEGIN_STATE;
do {
   switch ( state.getValue() ) {
   case BEGIN_STATE;
      state=OUT_STATE;
      break;
   case OUT_STATE:
      switch ( token.getValue() ) {
         case CODE_TOKEN:
            state = IN_STATE;
            output(token.string());
            break;
         case NEWLINE_TOKEN;
            output("<break>");
            output(token.string());
            break;
         ...
      }
      break;
   ...
   }
} while (state != END_STATE);

これはかなり面倒なので、通常はstateケースを別の機能に分割します。

于 2009-02-08T02:49:36.253 に答える
2

誰かがより良い例を持っていると確信していますが、Phil Haackによるこの投稿を確認できます。これには、正規表現と同じことを行うステートマシンの例があります（以前の投稿には、さらにいくつかの正規表現の例があります）おもう..）

そのページの「HenriFormatter」を確認してください。

于 2009-02-08T02:18:00.530 に答える
1

どの学術論文を読んだかはわかりませんが、有限状態マシンの実装方法を理解することはそれほど難しくありません。いくつかの興味深い数学がありますが、アイデアを理解するのは実際には非常に簡単です。FSM を理解する最も簡単な方法は、入力と出力を使用することです (実際、これは正式な定義のほとんどを構成するため、ここでは説明しません)。「状態」とは、本質的には、発生した、および特定の時点から発生する可能性のある一連の入力と出力を記述するだけです。

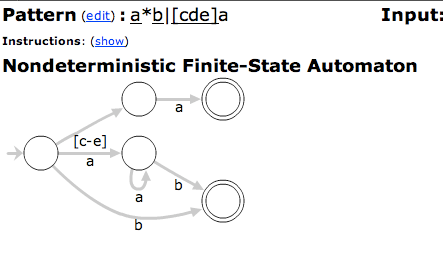
有限ステート マシンは、図で理解するのが最も簡単です。例えば：

代替テキスト http://img6.imageshack.us/img6/7571/mathfinitestatemachinedco3.gif

これが言っているのは、ある状態 q0 (横に開始記号がある状態) から開始すると、他の状態に移動できるということです。各状態は円です。各矢印は、入力または出力を表します (見方によって異なります)。有限状態マシンを考える別の方法は、「有効な」または「許容可能な」入力の観点からです。特定の有限状態マシンでは不可能な特定の出力文字列があります。これにより、式を「一致」させることができます。

ここで、q0 から開始するとします。ここで、0 を入力すると、状態 q1 に移動します。ただし、1 を入力すると、状態 q2 に移動します。これは、入出力矢印の上にある記号で確認できます。

q0 から開始して、この入力を取得するとします。

0、1、0、1、1、1

これは、状態を通過したことを意味します (q0 の入力はなく、そこから開始します)。

q0 -> q1 -> q0 -> q1 -> q0 -> q2 -> q3 -> q3

意味がわからない場合は、指で絵をなぞってください。q3 は、入力 0 と 1 の両方で自分自身に戻ることに注意してください。

これをすべて別の言い方で言うと、「状態 q0 にいて、0 が表示された場合は q1 に進みますが、1 が表示された場合は q2 に進みます。」各状態に対してこれらの条件を作成すると、状態マシンの定義がほぼ完了します。あなたがしなければならないのは、状態変数と、入力を送り込む方法を用意することだけです。それが基本的にそこにあるものです。

では、ジョエルの発言に関して、これがなぜ重要なのですか? さて、「すべてを支配する 1 つの真の正規表現」を構築することは非常に困難であり、変更を維持することや、他の人が戻ってきて理解することさえも難しい場合があります。また、場合によってはより効率的です。

もちろん、ステート マシンには他にも多くの用途があります。これが少しでも役立つことを願っています。あえて理論には触れませんでしたが、FSM に関する興味深い証拠がいくつかあります。

于 2009-02-08T02:43:52.600 に答える