二部グラフの場合、隣接行列をその二隣接行列と呼ばれるものに置き換えることができます。
部分が r 頂点と s 頂点を持つ 2 部グラフの隣接行列 A は、次の形式を持ちます。
A=OBBTO
_ _
ここで、B は r × s 行列、O はすべてゼロの行列です。明らかに、行列 B は二部グラフを一意に表し、一般にその二隣接行列と呼ばれます。
現在、DAG は 2 部グラフです。たとえば、トポロジー的に並べ替えて、セット U と V をそれぞれ奇数または偶数のトポロジー レベルにあるノードにすることができます。
これは、n 個のノードを持つ DAG の場合、 2行列ではなく(n/2) 2行列 (平均)のみが必要であることを意味します。問題は、それを構築する方法がわからないことです。ヒントはありますか？
すべての DAG が 2 部グラフであるとは限らないため、DAG の biadjacency 行列を構築することはできないと思います。
簡単な例を次に示します。3 つの頂点を持つ有向グラフを考え、それらを A、B、および C と表します。エッジは A を B、B を C、A を C に接続します。グラフは有向グラフであるため、明らかに DAG です。サイクルはありません (A->B->C<-A はサイクルではありません)。ただし、グラフは 2 部構成ではありません。A、B、および C を、同じセット内の頂点間にエッジがない 2 つの互いに素なセットに分割する方法はありません。
結論として、DAG であるが 2 部構成ではないグラフがあるため、すべての DAG が 2 部構成であるとは限りません。
DAG をトポロジ的に並べ替えて、頂点を 2 つの互いに素なセットに分割できるという事実は、同じセットの頂点間にエッジがないことを意味しないことに注意してください。
A 行列の双方向行列 B は、グラフが無向の場合にのみ構築できるようです。
ウィキペディアの例に基づく:
この DAG の隣接行列は次のようになります。
Blue -> Red
B = 1 1 0 0
0 0 1 0
0 0 0 0
0 0 0 0
0 0 0 1
Red -> Blue
C = 0 1 0 0 0
0 1 0 0 0
0 0 1 1 1
0 0 0 0 0
ご覧のとおり、C は B の転置ではありません。説明したように A 行列を作成することはできないようです。ただし、次のような A 行列を作成できます。
A = 0 B
C 0
これには 2 * (n/2)^2 のスペースが必要ですが、これは n^2 よりも優れています。
B 行列と C 行列を作成するには、U と V の各ノードを (それぞれ) ループして、アウトバウンド エッジを決定する必要があります。
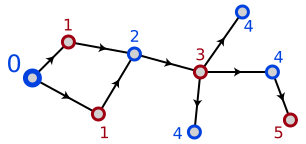
次のコードは、指定された隣接行列がバイパタイトの場合、その隣接行列を作成します (バイパタイト グラフのみがバイ隣接行列を持ちます)。指定されたグラフがバイパタイトでない場合、GetBiadjacencyMatrix() メソッドは null を返します。
Biadjacency マトリックスを含む提供されたサンプルのグラフ http://www.freeimagehosting.net/image.php?10e9b6a746.jpg
画像が見えませんか？ここをクリック
public class Matrix
{
private void Usage()
{
int[,] AdjacencyMatrix = new int[,] {
{0, 1, 1, 0, 0, 0, 0, 0, 0},
{1, 0, 0, 1, 0, 0, 0, 0, 0},
{1, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 1, 1, 0, 1, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 1, 1, 1, 0},
{0, 0, 0, 0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0, 1},
{0, 0, 0, 0, 0, 0, 0, 1, 0}
};
int[,] BiadjacencyMatrix = GetBiadjacencyMatrix(AdjacencyMatrix);
}
public static int[,] GetBiadjacencyMatrix(int[,] adjacencyMatrix)
{
int NodeCount = adjacencyMatrix.GetLength(0);
NodeInfo[] Nodes = new NodeInfo[NodeCount];
for (int c = NodeCount - 1; c >= 0; c--)
Nodes[c] = new NodeInfo(c);
if (ColorNode(adjacencyMatrix, Nodes, 0, 1, -1) != NodeCount)
return null; // Given graph is not bipatite.
int Part1Count = 0, Part2Count = 0;
foreach (NodeInfo Node in Nodes)
Node.IndexInPart = Node.PartID == 1 ? Part1Count++ : Part2Count++;
int[,] ToReturn = new int[Part1Count, Part2Count];
foreach (NodeInfo NodeInPart1 in Nodes)
if (NodeInPart1.PartID == 1)
foreach (NodeInfo NodeInPart2 in Nodes)
if (NodeInPart2.PartID == 2)
ToReturn[NodeInPart1.IndexInPart, NodeInPart2.IndexInPart]
= adjacencyMatrix[NodeInPart1.IndexInGraph, NodeInPart2.IndexInGraph];
return ToReturn;
}
private static int ColorNode(int[,] adjacencyMatrix, NodeInfo[] nodes, int currentNode, int currentPart, int parentNode)
{
if (nodes[currentNode].PartID != -1)
return nodes[currentNode].PartID != currentPart ? -1 : 0;
int ToReturn = 1;
nodes[currentNode].PartID = currentPart;
for (int c = nodes.Length - 1; c >= 0; c--)
if (adjacencyMatrix[currentNode, c] != 0 && c != parentNode)
{
int More = ColorNode(adjacencyMatrix, nodes, c, currentPart == 1 ? 2 : 1, currentNode);
if (More == -1) return -1;
ToReturn += More;
}
return ToReturn;
}
}
public class NodeInfo
{
private int _IndexInGraph;
private int _PartID;
private int _IndexInPart;
private bool _IsVisited;
public NodeInfo(int indexInGraph)
{
_IndexInGraph = indexInGraph;
_PartID = -1;
_IndexInPart = -1;
_IsVisited = false;
}
public int IndexInGraph
{
get { return _IndexInGraph; }
set { _IndexInGraph = value; }
}
public int PartID
{
get { return _PartID; }
set { _PartID = value; }
}
public int IndexInPart
{
get { return _IndexInPart; }
set { _IndexInPart = value; }
}
public bool IsVisited
{
get { return _IsVisited; }
set { _IsVisited = value; }
}
}