8

行き詰まったように感じます、友達。「Pearls of Functional Algorithm Design」の第 11 章 (「最大セグメント合計ではない」) から方程式を選ぶことを誰かが説明してくれますか?

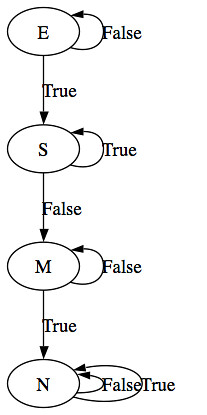
ここに問題があります (少し単純化されています) 与えられた遷移を持ついくつかの状態を考えてみましょう:

data State = E | S | M | N 
                deriving (Show, Eq) 

step E False = E 
step E True = S 
step S False = M 
step S True = S 
step M False = M 
step M True = N 
step N False = N 
step N True = N

それでは、pick を定義しましょう。

 pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

著者は、次の 7 つの方程式が成り立つと主張しています。

pick E xs = [[]]
pick S [ ] = [ ]
pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs)
pick M [ ] = [ ]
pick M (xs ++ [x ]) = pick M xs ++ pick S xs
pick N [ ] = [ ]
pick N (xs ++ [x]) = pick N xs ++ map (++[x]) (pick N xs ++ pick M xs)

誰か簡単な言葉で説明してくれませんか?なぜこれらの方程式が正しいのか、明らかな証明をどのように証明できるのでしょうか? S 方程式はほぼ理解できたように感じますが、全体としてこれはとらえどころのないままです。

4

1 に答える 1

18

わかりました、状態グラフを視覚化する必要がありました:

q7967337

そして、 の型シグネチャを与えpick :: State -> [[Bool]] -> [(State, [Bool])ます。

さて、これは最初の方程式と一致しませpick E xs = [[]]んpick E xs = [(E,[])]。

おそらく、次のように定義するつもりでしたpick。

pick :: State -> [[Bool]] -> [[Bool]]
pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

その定義を仮定すると、最初の式は意味を成します。で開始すると、で終了するEブール値の唯一のシーケンスは空のリストであると主張しています。xsE

[]これはεを仮定していることに注意してくださいxs。

また、もし , ならys = replicate n False、pick E [ys] = [ys]これは ∀ n, ys∉を意味しxsます。

2 番目、4 番目、および 6 番目の方程式はすべて の形式であり、これはおよびpick _ [ ] = [ ]の定義によって自明に成り立ちます。mapfilter

3 番目の式も、pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs)あまり意味がありません。私が推測しているのは、それが言おうとしているのは次のとおりです。

pick S (map (++[True] xs) = map (++[True]) (pick S xs ++ pick E xs)

つまり、 で始まり でE終わるパスは、 orSへの既存のパスを取得してを追加することで作成できます。同様に、で終わるすべてのパスは で終わらなければなりません。ESTrueSTrue

5 番目の方程式も同様に無意味であり、次のように記述します。

pick S (map (++[False] xs) = map (++[False]) (pick S xs ++ pick M xs)

そして、7 番目の式は次のように言い換える必要があります。

pick N (map (++ [True]) xs) = pick N xs ++ map (++[True]) (pick N xs ++ pick M xs)
于 2011-11-01T14:29:41.917 に答える