20

ポイントが特定の線に属しているかどうかはどうすればわかりますか？

可能であれば、例をいただければ幸いです。

4

10 に答える 10

30

最も単純な形式では、座標を直線の方程式に差し込んで等値をチェックするだけです。

与えられた:

Point p (X=4, Y=5)
Line l (Slope=1, YIntersect=1)

X と Y を接続します。

   Y = Slope * X + YIntersect
=> 5 = 1 * 4 + 1
=> 5 = 5

そうです、ポイントは線上にあります。

ラインが (X1,Y1),(X2,Y2) 形式で表されている場合、次の方法で勾配を計算できます。

 Slope = (y1 - y2) / (x1-x2)

そして、これで Y 交差を取得します。

 YIntersect = - Slope * X1 + Y1;

編集：Y交差を修正しました（これはX1 / Y1でした...）

x1 - x2ではないことを確認する必要があり0ます。そうである場合、ポイントがライン上にあるかどうかを確認することは、ポイントの Y 値が または に等しいかどうかを確認するだけx1ですx2。また、ポイントの X が「x1」または「x2」でないことを確認します。

于 2009-05-25T17:02:54.973 に答える
26

描画アプリケーションでこのチェックを使用するため、いくつかの追加要件を処理する関数を作成しました。

  • あいまいさ - 関数は行をクリックして行を選択するために使用されるため、エラーの余地があるはずです。
  • 線には EndPoint と StartPoint があり、無限の線はありません。
  • まっすぐな垂直線と水平線を処理する必要があります (x2 - x1) == 0 は、他の回答でゼロによる除算を引き起こします。
private const double SELECTION_FUZZINESS = 3;

internal override bool ContainsPoint(Point point)
{
    LineGeometry lineGeo = geometry as LineGeometry;
    Point leftPoint;
    Point rightPoint;

    // Normalize start/end to left right to make the offset calc simpler.
    if (lineGeo.StartPoint.X <= lineGeo.EndPoint.X)
    {
        leftPoint   = lineGeo.StartPoint;
        rightPoint  = lineGeo.EndPoint;
    }
    else
    {
        leftPoint   = lineGeo.EndPoint;
        rightPoint  = lineGeo.StartPoint;
    }

    // If point is out of bounds, no need to do further checks.                  
    if (point.X + SELECTION_FUZZINESS < leftPoint.X || rightPoint.X < point.X - SELECTION_FUZZINESS)
        return false;
    else if (point.Y + SELECTION_FUZZINESS < Math.Min(leftPoint.Y, rightPoint.Y) || Math.Max(leftPoint.Y, rightPoint.Y) < point.Y - SELECTION_FUZZINESS)
        return false;

    double deltaX = rightPoint.X - leftPoint.X;
    double deltaY = rightPoint.Y - leftPoint.Y;

    // If the line is straight, the earlier boundary check is enough to determine that the point is on the line.
    // Also prevents division by zero exceptions.
    if (deltaX == 0 || deltaY == 0) 
        return true;

    double slope        = deltaY / deltaX;
    double offset       = leftPoint.Y - leftPoint.X * slope;
    double calculatedY  = point.X * slope + offset;

    // Check calculated Y matches the points Y coord with some easing.
    bool lineContains = point.Y - SELECTION_FUZZINESS <= calculatedY && calculatedY <= point.Y + SELECTION_FUZZINESS;

    return lineContains;            
}
于 2012-12-06T10:37:50.860 に答える
21

点 R = (rx, ry) が点 P = (px, py) と Q = (qx, qy) を結ぶ線上にあるかどうかを判断する最良の方法は、行列式が

{{qx - px, qy - py}, {rx - px, ry - py}},

つまり、(qx - px) * (ry - py) - (qy - py) * (rx - px) は 0 に近いです。このソリューションには、投稿された他のソリューションよりもいくつかの関連する利点があります。まず、垂直線に特別なケースは必要ありません。 2 つ目は、除算を行わない (通常は処理が遅い) ことです。

于 2009-05-25T17:31:34.283 に答える
7

ライン上の2つのポイントとテストするポイントが与えL0られL1ますP。

               (L1 - L0) * (P - L0)
n = (P - L0) - --------------------- (L1 - L0)
               (L1 - L0) * (L1 - L0)

ベクトルのノルムは、線からとまでnの点の距離です。この距離がゼロまたは十分に小さい場合（丸め誤差の場合）、ポイントは線上にあります。PL0L1

記号*は内積を表します。

例

P = (5, 5)

L0 = (0, 10)
L1 = (20, -10)

L1 - L0 = (20, -20)
P  - L0 = (5, -5)

              (20, -20) * (5, -5)
n = (5, -5) - --------------------- (20, -20)
              (20, -20) * (20, -20)

              200
  = (5, -5) - --- (20, -20)
              800

  = (5, -5) - (5, -5)

  = (0, 0)
于 2009-05-25T17:17:24.767 に答える
6

パトリック・マクドナルド氏がほぼ正しい答えを出したと思います。これが彼の答えの訂正です。

public bool IsOnLine(Point endPoint1, Point endPoint2, Point checkPoint)
{
    return (((double)checkPoint.Y - endPoint1.Y)) / ((double)(checkPoint.X - endPoint1.X))
        == ((double)(endPoint2.Y - endPoint1.Y)) / ((double)(endPoint2.X - endPoint1.X));
}

もちろん、他にも多くの正解、特にジョシュさんがいますが、これが最良の答えだと思いました。

evryoneに感謝します。

于 2009-05-25T18:07:51.933 に答える
4 
y = m * x + c

これが直線の方程式です。x & y は座標です。各線は、その傾き (m ) と y 軸との交点 (c) によって特徴付けられます。

したがって、直線の m & c が与えられた場合、式が x = x1 および y = y1 に当てはまるかどうかを確認することで、点 (x1, y1) が直線上にあるかどうかを判断できます。

于 2009-05-25T17:00:36.113 に答える
3

2D ラインは一般に、2 つの変数 x と y の方程式を使用して表されます。ここでの方程式はよく知られています。

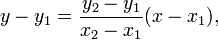
y-y1 = (y1-y2)/(x1-x2) (x-x1)

ここで、GDI+ の線が (0,0) から (100, 100) に描画され、m=(0-100)/(0-100) = 1 の値が描かれていると想像してください。したがって、線の式は y-0=1 です。 *(x-0) => y=x

問題の線の方程式が得られたので、ポイントがこの線に属しているかどうかを簡単にテストできます。x=x3 と y=y3 を代入したときに直線方程式を満たす場合、与えられた点 (x3, y3) はこの直線に属します。たとえば、点 (10, 10) は 10=10 であるためこの線に属しますが、(10,12) は 12 != 10 であるためこの線に属しません。

注: 垂直線の場合、勾配 (m) の値は無限大ですが、この特殊なケースでは、垂直線の方程式を直接 x=c (c = x1 = x2) で使用できます。

これが最も効率的な方法であるかどうかはわかりません。もう少し時間があるときに、より効率的な方法を見つけようとします。

お役に立てれば。

于 2009-05-25T17:11:51.280 に答える
3

端点で定義された線がある場合

PointF pt1, pt2;

そして確認したいポイントがあります

PointF checkPoint;

次に、次のように関数を定義できます。

bool IsOnLine(PointF endPoint1, PointF endPoint2, PointF checkPoint) 
{
    return (checkPoint.Y - endPoint1.Y) / (endPoint2.Y - endPoint1.Y)
        == (checkPoint.X - endPoint1.X) / (endPoint2.X - endPoint1.X);
}

次のように呼び出します。

if (IsOnLine(pt1, pt2, checkPoint) {
    // Is on line
}

ただし、ゼロ除算を確認する必要があります。

于 2009-05-25T17:15:59.043 に答える
1

直線の方程式は次のとおりです。

y = mx + c

したがって、この方程式を満たす場合、点(a,b)はこの線上にあります。b = ma + c

于 2009-05-25T17:06:08.510 に答える
0

メソッドの代替として、slope/y-intercept次を使用してこのアプローチを選択しましたMath.Atan2。

// as an extension method
public static bool Intersects(this Vector2 v, LineSegment s) {
    //  check from line segment start perspective
    var reference = Math.Atan2(s.Start.Y - s.End.Y, s.Start.X - s.End.X);
    var aTanTest = Math.Atan2(s.Start.Y - v.Y, s.Start.X - v.X);

    //  check from line segment end perspective
    if (reference == aTanTest) {
        reference = Math.Atan2(s.End.Y - s.Start.Y, s.End.X - s.Start.X);
        aTanTest = Math.Atan2(s.End.Y - v.Y, s.End.X - v.X);
    }

    return reference == aTanTest;
}

最初のチェックreferenceでは、線分の始点から終点までの arcTan が決定されます。次に、始点の観点から、ベクトルに対する arcTan を決定しvます。

これらの値が等しい場合は、エンドポイントの観点からチェックします。

シンプルで、水平、垂直、およびその間のすべてを処理します。

于 2016-04-01T20:31:06.307 に答える