Delaunay三角形分割がそのステップである、内側軸抽出の実装を必要とするプログラムを書いています。外部内側軸は不要であるため、対応する外部三角形を削除する予定です。幸いなことに、多くの図が掲載されたページに出くわしました。また、内部および外部の Delaunay 三角形を決定する方法のヒント (「破線の周囲に基づく」) もありましたが、詳細な説明はなく、ヒントにすぎません。アルゴリズムを知っている人はいますか？
編集:最初の点が閉じた多角形の境界からサンプリングされることを忘れていました。私の意図は、各ドローネ三角形が多角形の内側にあるかどうかを判断することです。
このソリューションでは、 CGALと同じように「仮想無限 Delaunay 頂点」を使用して Delaunay 三角形分割を表すデータ構造があることを前提としています(詳細はこちらを参照)。
アイデアは、境界 Delaunay エッジを見つけることです。2 つの連続するサンプル ポイントを接続するエッジです。次に、ドロネー三角形分割を「フラッド」して、ドロネー面を分類します。無限頂点は外部であることを知っているので、境界エッジを交差しない限り、その隣接 (および隣接の隣接など) を外部として分類できます。境界エッジに到達した場合は、単純に隣接する三角形を内部としてマークし、同様に続行できます。
入力: 閉じた形状の境界を高密度にサンプリングした点の集合。
出力: 形状の内部のボロノイ図 (形状の中心軸の近似値)
このような入力の場合
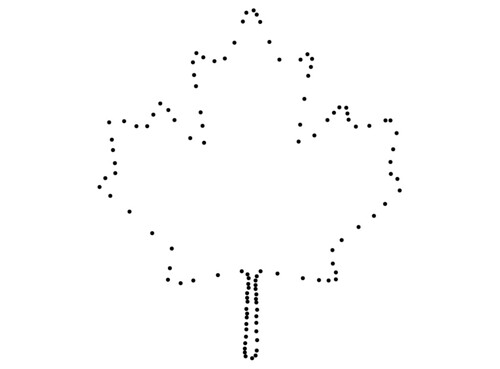
、次の中心軸近似を計算できます。
Mesecinaの無料の Windows バイナリを使用して、この中心軸近似が実際にどのように動作するかを確認できます。ソースコードはこちら。
外部三角形を作成しない別の形式の三角形分割の使用を検討しましたか? 私はかつて、多角形の三角形分割の理論的側面について議論するために多くの時間を費やしたコースを受講しました。コースのサイトをざっと見てみると、いくつかの洞察が得られるでしょうか? http://cgm.cs.mcgill.ca/~godfried/teaching/cg-web.html#triangulation
編集：実際には、私は別のことを考えていました. 三角測量しようとしている多角形が既にある場合は、グリーンの定理を使用できます。グリーンの定理は、多角形の周囲を使用してその面積を計算します! さらに重要なことは、この場合、点が線の片側にあるのか、それとも別の側にあるのかを、面積の符号を見ることで判断できることです。多角形では、グリーンの定理は単純な引き算の問題になります。したがって、多角形の内側にあることがわかっている任意の点を取り、多角形の各エッジに対する面積を計算します。これにより、各線のどちら側にポイントを配置する必要があるかがわかります。次に、各三角形の内側に点を取り、同じことを行います。いずれかの符号が間違っている場合は、外部三角形があります。(注: ポリゴンの形状によっては、これが実際に機能しない場合があります。
彼らが提示するアルゴリズムは、彼らの図の 1 つに示されているように、少し壊れているように見えます。これが、Google Scholar に有用な引用がないように見える理由かもしれません.
おそらく、私はここであまりにも多くの仮定を立てていますが、ポイントの束で構成される多角形があり、それらのポイントを三角形分割しているように聞こえます。次に、ポリゴンの外側にあるすべての三角形を破棄したいと思いますよね?
外部三角形を作成しないように、(モノトーン分解または類似のものを使用して) 多角形を三角形化しないのはなぜですか? これにより実行時間が長くなる可能性があると思います（最初にO（nlogn）時間で三角測量を行い、次にO（n ^ 2）時間でドローネー三角測量を作成します）が、より高速な方法があるかもしれません。
