algorithm - ニュートンラフソンの初期推定

Question

Ax+Bsin(x)=CA、B、Cの観点から方程式の初期推定値を決定するにはどうすればよいですか？ニュートンラフソンを使用してそれを解決しようとしています。A、B、およびCは実行時に指定されます。

この目的のためにニュートンラフソンよりも効率的な方法は他にありますか？

Answer 1

最適な初期推定はルート自体であるため、「最適な」推測を見つけることは実際には有効ではありません。

任意の推測は、任意の整数f'(x0) != 0のゼロでのみ発生する任意のステップである限り、最終的に有効な解を提供します。cos(x)k*pi + pi/2k

それが機能するかどうかを確認するために、試してみx0 = C * piます。

ただし、最大の問題は、関数の周期的な性質です。ニュートン法は、何度も前後sin(x)にシフトするので、関数に対して遅くなります（それが機能する場合でも） 。x0

---

予防措置：

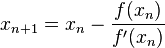
f'(xn)ニュートン法では、分母がどのようになっているのかわかりますか？何度も無限f'(x)に近づきます。0あなたのf'(x) = 0.0001（または発生する可能性のあるゼロに近い場所）の場合、あなたxn+1は本当に遠くに投げられますxn。

さらに悪いことに、これは周期関数であるために何度も発生する可能性があります。f'(x)つまり、ニュートン法は任意のに対して収束することさえない可能性がありx0ます。

Answer 2

最も単純な「適切な」近似は、sin（x）がほぼゼロであると仮定することです。したがって、次のように設定します。

x0 = C/A

Answer 3

さて、A、B、Cが実数で、0とは異なる場合、(B+C)/Aは最高のルートへの上位引用符(C-B)/Aであり、最低のルートへの下位引用符-1 <= sin(x) <= 1です。あなたはそれらから始めることができます。

Answer 4

ニュートン法は、どのような推測でも機能します。問題は単純です。方程式があり、x0 = 100と推測し、その最良の近似解はx0 = 2であり、世界の推測を使用すると、答えは2.34 *であり、最終的には2.34*になります。メソッドは、有効な推測がないと、快適ではない多くの解決策が必要になるため、推測を選択するように指示します。この方法を20回繰り返すことは誰も望んでおらず、解決策を推測することは難しくありません。たとえば、3も重要なポイントを見つけるだけです。大きくて2は小さすぎるので、答えは2から3の間ですが、代わりに2を推測すると、50を推測しても正しい解決策が得られます。