8

コンピューティング、特に円周率の無限の数に興味があります。

コンピューターが円をレンダリングするには、円周率を理解する必要があります。しかし、それが無限である場合、どうすればよいでしょうか？

私はこれを調べすぎていますか？丸められた値を使用するだけでしょうか？

4

10 に答える 10

15

数学的には、コンピューターは有限で非連続的であるため、PIを完全に知ることも、正しく円を描くこともできません。

ただし、デジタル領域では、これらはいずれも存在しないため、PIを概算し、それを使用して円を概算するだけで十分です。結果として、正確なPIから計算されたピクセルとまったく同じピクセルになります。

いずれにせよ、結果のピクセルも実際には円ではありません。これは、デジタルポイントの有限のコレクションであり、円は無限の数のポイントで構成される曲線であり、ほとんどが不合理な値であるためです。

（PIは通常、円をプロットするために使用されないことが指摘されていますが、これは事実ですが、円をプロットするために使用される方法は、PIの値を表現および/または計算するために使用される式に関連しています。まだ同じ問題があります）。

于 2009-07-27T22:16:17.560 に答える
7

一般的には概算で十分です。円を「レンダリング」するには、コンピューターは、必要な解像度（有限）で正確にレンダリングするのに十分な円周率を理解するだけで済みます。

編集：他の人が指摘しているように、円をレンダリングするのに円周率も必要ありません。それでも、質問の要点は「コンピューターは円周率のような数字をどのように扱うのか」でした。それらは近似を使用し、それらの近似を使用する人は誰でも、それらが与えられた目的に対して十分に正確であるかどうかを決定しなければなりません。

于 2009-07-27T22:06:48.203 に答える
6

円を描くのに円周率はまったく必要ありません。円を描く方法はたくさんあります。素朴な方法は、サインとコサインを使用することです。

私が8ビットマシンで最も頻繁に見たアルゴリズムはブレゼンハムの円でした。そのために浮動小数点演算も必要ありません。

于 2009-07-27T22:35:20.953 に答える
2

コンピューターは、円周率の適切な近似値を使用します。

System.Math.PIに関するMSDNの記事から

このフィールドの値は3.14159265358979323846です。

ところで：PIは無限ではありません。これは不合理です。つまり、循環小数の桁数が無限になります。PIには、非常に短い式がいくつかあります。（詳細については、ウィキペディアのページを参照してください）

PIの素晴らしく短い表現は次のとおりです。

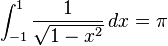
インテグラルとしてのPI

于 2009-07-27T22:06:58.623 に答える
2

プログラミング言語は、円周率および同様の「無限」数に丸められた定数を使用します。

より高い精度を得るには、必要な限りループされる反復アルゴリズムを使用します。

于 2009-07-27T22:26:30.347 に答える
2

宇宙の周りをミリメートルの精度で円を描くには、100桁未満の円周率が必要であるという証拠をどこかで見ました。つまり、手に時間がかかりすぎる人が計算した桁数よりもはるかに少ない桁数です。計算能力が多すぎます...）。さて、もし私がその証拠を見つけることができれば...（編集）それを見つけた

于 2009-07-28T01:27:02.067 に答える
1

非常に少数に丸められ、おそらく定数であると思います。PHPを使用する場合、PIは次のようにレンダリングします。

エコーpi（）; // 3.1415926535898
エコーM_PI; // 3.1415926535898

高校で必要なのは3.14159だけであるのと同じように、コンピューターはそれをかなり正確にするために必要なのはそれだけです。

于 2009-07-27T22:08:05.283 に答える
1

もちろん、科学計算などの特別な場合を除いて、コンピューターは円周率の丸められた値を使用します。たとえば、Pythonではpiは次のように表されます。

>>> import math
>>> math.pi
3.1415926535897931

IDLE、pythonsインタラクティブインタプリタでこれを自分でテストできます。

于 2009-07-27T22:08:50.790 に答える
1

このサイトの方法を使用する場合でも、別のサイトの方法を使用する場合でも、近似値は「十分に良い」ことがよくあります。

「レンダリング」は別の問題です。画面解像度が有限の場合、πの完全な値はそれほど重要ではありません。

更新：計算は、レンダリングとは別の問題である可能性があります。一部のアプリケーションでは、標準のdoubleよりも高い精度が必要になる場合があります。問題によって異なります。

于 2009-07-27T22:10:11.287 に答える
1

円周率は無限ではありません。それは不合理です。つまり、商として表現することはできません。桁数は無限大です。 http://en.wikipedia.org/wiki/Proof_that_π_is_irrational

コンピューティングについては、ここでいくつかの情報を見つけてください。 http：//en.wikipedia.org/wiki/Computing_π

素敵なページもこちら http://3.141592653589793238462643383279502884197169399375105820974944592.com/

于 2009-07-27T22:46:20.777 に答える