2

任意の二分木が与えられていると仮定します。すべてのノードに次のことが当てはまる場合、ツリーをバランスの取れたものと呼びます。

  1. そのノードはリーフ、または
  2. 左側のサブツリーの高さと右側のサブツリーの高さの差は最大で±1であり、左右のサブツリー自体のバランスが取れています。

ツリーのバランスをとるためにツリーに追加する必要のあるノードの最小数を決定するための効率的なアルゴリズムはありますか？簡単にするために、ノードはリーフノードとしてのみ挿入できると仮定します（ノードがリバランスを行わない二分探索木に挿入される方法のように）。

4

3 に答える 3

2

次のツリーはあなたの定義に当てはまりますが、私にはあまりバランスが取れていないようです。

深さ5

編集この答えは間違っていますが、まだ削除したくないほど興味深いものが含まれています。アルゴリズムはバランスの取れたツリーを生成しますが、最小のツリーは生成しません。追加するノードの数は次のとおりです。

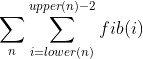
ここで、n範囲はツリー内のすべてのノードにまたがり、lower(n)はnより低い深さupper(n)の子の深さであり、はより高い深さのの子のn深さです。k最初のフィボナッチ数の合計がであるという事実を使用してfib(k+2)-1、内部の合計を。に置き換えることができfib(upper(n)) - fib(lower(n) + 2)ます。

式は（多かれ少なかれ）次のアルゴリズムから導出され、ツリーにノードを追加して、バランスを取ります（Pythonでは、関連するアルゴリズムのみを表示します）。

def balance(tree, label):
  if tree is None:
    return (None, 0)
  left, left_height = balance(tree.left_child, label)
  right, right_height = balance(tree.right_child, label)
  while left_height < right_height - 1:
    left = Node(label(), left, balanced_tree(left_height - 1, label))
    left_height += 1
  while right_height < left_height - 1:
    right = Node(label(), right, balanced_tree(right_height - 1, label))
    right_height += 1
  return (Node(tree.label, left, right), max(left_height, right_height) + 1)

def balanced_tree(depth, label):
  if depth <= 0:
    return None
  else:
    return Node(label(),
                balanced_tree(depth - 1, label),
                balanced_tree(depth - 2, label))

要求に応じて：ツリーを作成する代わりにカウントを報告します。

def balance(tree):
  if tree is None:
    return (0, 0)
  left, left_height = balance(tree.left_child)
  right, right_height = balance(tree.right_child)
  while left_height < right_height - 1:
    left += balanced_tree(left_height - 1) + 1
    left_height += 1
  while right_height < left_height - 1:
    right += balanced_tree(right_height - 1) + 1
    right_height += 1
  return (left + right, max(left_height, right_height) + 1)

def balanced_tree(depth):
  if depth <= 0:
    return 0
  else:
    return (1 + balanced_tree(depth - 1)
              + balanced_tree(depth - 2))

編集：実際には、深さnの最小バランスツリーのサイズをより効率的に計算する（つまり、メモ化するか、閉じた形式を使用する：それはただfibonacci(n+1)-1）以外は、おそらくあなたが得ることができるのと同じくらい効率的だと思います。バランス状態をテストするためにツリー内のすべてのノードを調べます。そのアルゴリズムはすべてのノードを正確に1回調べます。

于 2013-01-18T04:11:00.803 に答える
1

これは機能しますか？

上から再帰的に移動します。ノードAのバランスが崩れている場合は、ノードAのバランスがとれるまで、短辺にノードBを追加し、ノードBに十分な数の左側ノードを追加します。

（もちろん、追加されたノードを数えます。）

于 2013-01-18T02:14:25.707 に答える
1

まず、各ノードの左の子と右の子の高さを見つけましょう。

ここで、木の根を考えてみましょう。その高さは

1+max(height(root.left) , height(root.right))。

左の高さがn-1で、右の高さが最小n-2であると仮定します。ここで別の関係を定義しましょう。req[node]->ツリーのバランスをとるために必要な各ノードの最小の高さ。

ノードの高さが観察される場合、hその子の1つは少なくともn-1である必要があり、バランスをとるために、他の子は少なくともn-2である必要があります。

req[root]=ルートの高さでルートから開始

擬似コードは次のとおりです。 

    def chk_nodes(root, req):

      if(root == NULL):
        return minNodes(req)

      if(left[root] > right[root]):
       return chk_nodes(root.left  , req-1) + chk_nodes(root.right , req-2)

      else return chk_nodes(root.left , req-2) + chk_nodes(root.right , req-1)

では、minNodes（int req）とは何ですか？

これは、「高さhの平衡二分木を作成するために必要なノードの最小数」を返す関数です。機能は非常に直感的で自明です。

      def minNodes(int req) :
          if req < 0 : return 0
          return 1 + minNodes(req-1) + minNodes(req-2)

minNodes関数では、ルックアップテーブルを使用して、ルックアップ時間をO（1）ルックアップ時間にし、構築のためにO（N）にすることができます。

chk_nodes関数が再帰的に実行されると、リーフノードでは左ノードのreqが残ります。そのreq>0の場合、高さreqの新しいサブツリー（バランス）が存在するはずです。したがって、この特定のリーフノードではminNodes（req）が必要です。

たった2回のトラバーサルとO(N)時間でO(N)、問題は解決されます。

于 2020-03-30T15:36:51.223 に答える