tree - 有向非巡回グラフの強さを判断する方法は?

Question

有向非巡回グラフの強度、特に特定のノードの強度を判断するための堅実なアルゴリズム/アプローチとして認識されているものは興味深いものです。これに関する主な質問は、次の 2 つのグラフに要約できます。

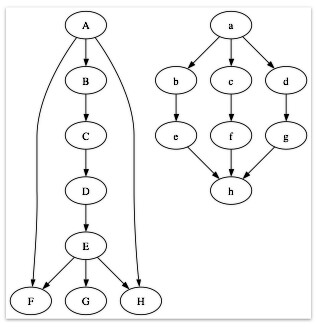(グラフが表示されない場合は、ここをクリックするか、次のリンクにアクセスしてください: http://www.flickr.com/photos/86396568@N00/2893003041/

私の目には、A は A よりも強い立場にあります。リンクがノックアウトされた場合に、ノードがどれだけ強く残るかで強さを判断しています. 最初のものは細い「竹馬」、2番目のものは太い「茎」と呼んでいます。

ノードの強さを判断するためにこれまでに検討したアプローチは次のとおりです。

1) 下のノードの数をカウントし、上のノードの数を引きます。

• A=7、a=7、B=5、b=1

2) 各ノードの (終端までの) 完全なパスの数を数え、それらの長さを合計します。

• A=17 (1+5+5+5+1)、B=12 (4+4+4)、a=9 (3+3+3)、b=2
• これにより、茎ではなく支柱が強くなります。

3) すべての可能なパスを数え、すべてのノードを宛先として扱います。

• A=9 (A->B、A->C、A->D、A->E、A->G、2xA->F、2xA->H)、B=6、a=9、b= 2

これまでのところ、3 が最良の選択肢のように思えますが、DAG 用に一般化された、より優れた選択肢はありますか? これは既知の最善のアプローチを持っているものですか？原則は、グラフ内のできるだけ多くの情報を使用し、解決策を直感的に説明できるようにすることです。

Answer 1

これは、強さの意味によって異なります。情報を表現する DAG の汎用性により、複数の結果の制御フローから、非副詞的談話接続詞の引数節、さらには文内の異なる単語間の依存関係の完全なセットまで、あらゆるものについて議論することができます。

これらはすべて、ノードの強度を異なる方法で表示します。たとえば、制御フローは、ダイアグラムの最終的な結果に対して最大の力を持っているため、結果の量が最も多いノード (したがって、最も外側のアーク) を最も強いノードと見なす場合があります。談話では、最強のノードは談話接続詞ですが、音声とテキストでは、最初の接続詞の後、3 番目の接続詞の前に見られます。文の語彙的な「頭」の選択は、それと直接相互作用するアークの量とは直接関係ありません。

私が理解しているのは、「強さ」という用語の多義的な性質と DAG が適合するデータの種類のために、このデータ型の「強さ」を計算するための真の万能薬はないということです。機械学習の問題では、これら 3 つのアプローチはすべて、分類またはランキングの問題で特定のタイプのノードを選択する際に非常に有益であると言えますが、最終的には、答えはデータ タイプの実際のアプリケーションに依存します。

Answer 2

「強さ」をもっと明確に定義する必要があると思います。これは最大流量の問題に関連していますか?

Answer 3

予測を行う場合、最善の策はおそらく最大エントロピー ランキング アルゴリズムになるでしょう。問題は、学習者にとって十分な大きさのデータ セットを作成することです。ゲームの各週の順位を 1 つのランキング インスタンスとして使用できるようです。

Answer 4

さて、実用的なアプリケーションはスポーツ チームです。各ノードはチームであり、各リンクは別のチームに対する勝利です。A->B->C->A のような円形の勝利パスはないと仮定します。目的は、グラフと競合しないパワー ランキングを取得することであり、チームの強さの順にチームをランク付けします。問題のサイトは、私の (やや皮肉っぽい) サッカー サイトhttp://beatpaths.com/です。では、NFL シーズン全体の完全なグラフを毎週見ることができます。(および他のスポーツ。) 基本的に、上に挙げたもの以外のランキング アルゴリズムを探しています。これは、グラフ内のすべての情報を使用することで、より意味があり、弁護できる可能性があります。目標は、将来のピックに関して必ずしもより正確になることではありませんが (より強力なアルゴリズムはおそらくそうなるでしょう)、これまでのシーズンをできるだけ合理的に説明することです.

サイトで NFL シーズンの第 3 週を確認できます。あいまいだった 2 つの「ビートループ」(長い話) を削除し、グラフの残りの部分に基づいて序列を決定しました。