6

これまでのところ、Fabrice Bellard の基数 2 の方程式が進むべき道のようです。

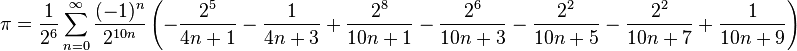
代替テキスト

皮肉なことに、これには BigReal 型が必要になります。これは .Net 用ですか? .Net 4.0 には BigInteger があります。

Haskell のバージョンを持っている人はいますか?

4

4 に答える 4

6

Haskellバージョンを求めているので、ここにJerzy Karczmarczukによる「πを計算するための世界で最も信頼性の低い手法」と呼ばれる論文があります：

このペーパーは、怠惰な関数型コーディングの非定型的な演習であり、楽しみと指導のために書かれています。プログラミング言語Haskellを理解している人なら誰でも読んで理解することができます。πのベイリー-ボールウェイン-プルエ式を、3、1、4、1、5、9の数字を生成する、共再帰的で増分的な方法で実装する方法を示します。。メモリがなくなるまで。誰かが多くの桁を必要とする場合、これは先に進む方法ではありません！私たちのコーディング戦略はひねくれた危険なものであり、間違いなく壊れています。これは、整数ベースで展開された適切な分数を表す数字の無限シーケンスのドメインでの算術に基づいています。操作方法を示します。加算、整数の乗算など、左から右へのシーケンスを無限に追加します。これは、あいまいさのために、すべての場合に明らかに機能するとは限りません。いくつかの深い哲学的結果は結論で議論されています。

これは、効率的または非常に実用的な方法で問題を実際に解決するわけではありませんが、面白く、怠惰な無限精度の演算に関する問題のいくつかを示しています。

それから、ジェレミー・ギボンズによるこの論文もあります。

于 2009-10-06T20:12:59.540 に答える
5

私のお気に入りの pi 用 Haskell スピゴットは、Jeremy Gibbons によるものです。

pi = g(1,0,1,1,3,3) where
    g(q,r,t,k,n,l) = 
        if 4*q+r-t<n*t
        then n : g(10*q,10*(r-n*t),t,k,div(10*(3*q+r))t-10*n,l)
        else g(q*k,(2*q+r)*l,t*l,k+1,div(q*(7*k+2)+r*l)(t*l),l+2)

その実装を正当化する数学的背景は、次の場所にあります。

Pi の桁の Spigot アルゴリズム

于 2009-10-13T14:55:50.793 に答える
2

DLRベースの動的言語 (例: IronPython )で大きな有理数を処理する可能性が存在します。または、 P/Invokeを介して大きな実数の移植可能な C/C++ 実装を使用できます。

于 2009-10-06T18:12:16.383 に答える
2

ウィキペディアでは、ここで pi の数値近似を取得する多くの方法について詳しく説明しています。彼らはまた、いくつかのサンプル擬似コードを提供します

編集：関連する現実世界の問題を解決することなく、この種の数学的問題に興味がある場合（これは間違いなく良い態度です、IMHO）、オイラープロジェクトのページにアクセスできます

于 2009-10-06T07:58:22.840 に答える