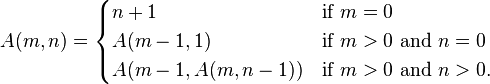論文に書きたい小さなアルゴリズムがいくつかあります。それらは比較的短く、簡潔です。ただし、それらを疑似コード (Cormen または Knuth 風) で記述する代わりに、それらの代数表現 (より線形でより優れた LaTeX レンダリング) を記述したいと思います。ただし、何かあれば、これに最適な表記法に関するリソースを見つけることができません。たとえば、ループをどのように表すのですか? もしも？リストへのタプルの追加?
この問題に遭遇し、どうにかして解決した人はいますか?
ありがとう。
編集：ありがとう、人々。質問の言い回しが下手だったと思います。もう一度言いますが、より明確にすることを願っています: 数学表記でループと if-then 句について話すための一般的な表記法は何ですか? たとえば$acc \leftarrow acc \cup \langle i,i+1 \rangle$、リストの「追加」メソッドを表すために使用できます。
これをしないでください。あなたは、人々がアルゴリズムに関する論文を読んだときに期待するものから逸脱しています。予想される慣行に従う必要があります。あなたのアイデアは、それに値する注目を集める可能性が高くなります。ローマにいるときは、ローマ人がするようにしなさい。
LaTeXed ペーパーのコード (または疑似コード) のフォーマットは非常に簡単です。たとえば、LaTeX でコードをフォーマットする を参照してください。
数学表記のif式はかなり頻繁に見られます。ループの通常のことは、漸化式、または同等に、再帰的に定義された関数です。
たとえば、ウィキペディアでアッカーマン関数がどのように定義されているかを次に示します。
この画像は、数学的な味わいを感じながらも、ほぼ正確に記述されたとおりに入力して実装できるので便利です。それを達成できるとは限りません。
ループに対応する他の数学表記には、∑-合計の表記と集合の内包的表記が含まれます。
これがあなたの質問に答えることを願っています！しかし、あなたの目的が何かがどのように行われるかを説明し、誰かに理解してもらうことである場合、数学者が方程式を見ることを好むと仮定するのはおそらく間違いだと思います。私はそれらが交換可能なツールだとは思いません（Turingの同等性にもかかわらず）。アルゴリズムに可変データ構造が含まれている場合、手続き型コードは、それを説明するための方程式よりも優れている可能性があります。
一般的なループのシンボルは存在しません。通常、合計演算子を使用します。「if」は含意を使用して表され、「リストにタプルを追加する」には、unionを使用します。
ただし、一般に、少し冗長性があることは必ずしも悪いことではありません。特に複雑なアルゴリズムの場合は、例や図を使用して、わかりやすい英語で説明するのが最適な場合があります。これは、非コーダーにも二重に当てはまります。
考えてみてください。ユークリッドの互除法に関する数学の教科書、またはエラトステネスのふるいを読むとき、それはどのように書かれていますか？通常、アルゴリズム自体は散文ですが、アルゴリズムの証明は数学記号が存在する場所です。
私はクヌートをコピーします。コンピューター サイエンスの環境で、彼ほどコミュニケーションの取り方を知っている人はほとんどいません。
Lisp は、講師がチューリング マシンよりも優れたツールを使用できるように、コンピューティング モデルの数学的表記法として始まりました。偶然にも、アセンブリで実装できることが判明しました。このようにして、プログラミング言語 Lisp が誕生しました。
しかし、Lisp が記述している計算モデルにはループがないため、これは実際にあなたが探しているものではないと思います: 代わりに再帰が使用されます。構文は代数から派生したもので、中かっこはこれを評価して結果を代用することを示します。実際、Lisp のコンピューティング モデルは基本的に代入です。つまり、本質的に代数です。
実際、Lisp、Haskell、Erlang などのほとんどの関数型言語は、数学から派生しています。Haskell は、ラムダ計算を使用して型システムを実装できることを証明した結果です。つまり、Haskell は、Lisp と同様に、純粋数学から生まれました。しかし、繰り返しになりますが、構文はおそらく慣れ親しんだものではありません。
確かに Lisp と Haskell の構文を数学者に説明でき、彼らはそれを「ゲーム」として扱うでしょう。ループ、再帰、条件分岐などの言語構造は、他の言語のようにやみくもに実装するのではなく、ゲームのルールから外して証明できます。これは、数学の別の分野であるコンビナトロニクスの領域にあなたを導きます。実際、コンビナトロニクスでは、数の概念でさえ、言語のネイティブな部分ではなく、ゲームのルールから構築できます (google Church Numerals)。
必要に応じて、Lisp/Scheme、Erlang、Haskell を調べてください。Erlang には特に、必要なものに近い構文があります。
add(a,b) -> a + b
ただし、C ライクな疑似コードで記述することをお勧めします。これは、プログラミング言語の最小公分母のようなものです。理解しやすくきれいな構文を持っています。また、関数の構文は、数学の関数からも派生しています。覚えていf(x)ますか？
プラスとして、数学者は C を書くことに慣れており、統計学者は C を書くことに慣れていますが (一般的には R を好みます)、物理学者は C を書くことに慣れており、プログラマーは少なくとも C を見ることに慣れています (私は、 C）に触れた。
実際、それをスクラッチします。あなたのターゲットオーディエンスは統計学者だとおっしゃいました。Rで書く
Haskell を見てみましょう。Haskell は latex で適切にフォーマットされ、優れた代数構文を備えています。また、コードが と でラップされていれば、Haskell を含む latex ファイルをコンパイルすることもでき\begin{code}ます\end{code}。ここを参照してください: http://www.haskell.org/haskellwiki/Literate_programming . おそらく、他の言語用の読み書き可能なプログラミング ツールがあります。
このウェブサイトの説明のようなものですか？
APL ? 唯一の問題は、それを読める人がほとんどいないことです。