これは、こちらの質問と同様の質問です。
サーフェスを定義する 3D 座標のリスト ( Point3D1、Point3D2、など) が与えられた場合、サーフェスの重心Point3D3を計算する方法は?
2D では、計算は次の式で与えられます。

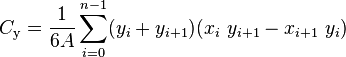
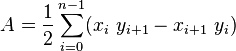
3Dアナログはどうですか?
これは、こちらの質問と同様の質問です。
サーフェスを定義する 3D 座標のリスト ( Point3D1、Point3D2、など) が与えられた場合、サーフェスの重心Point3D3を計算する方法は?
2D では、計算は次の式で与えられます。

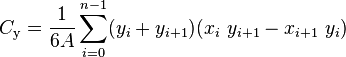
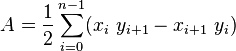
3Dアナログはどうですか?
ポイントを反時計回りにv 0、v 1、...、v Nとする。ここで、v i = (x i , y i , z i )。
次に、トリプレット (v 0 , v 1 , v 2 ), (v 0 , v 2 , v 3 ), ..., (v 0 , v i , v i+1 ), ..., (v 0 , v N-1 , v N ) は、多角形を作成する N-1 個の三角形を形成します。
各三角形の面積は| (v i − v 0 ) × (v i+1 − v 0 ) | ÷ 2、ここで、× は外積、| · | はベクトルの長さです。
凹んだ部分を補正するために、面積を負にする必要がある場合があります。簡単なチェックは、(v i − v 0 ) × (v i+1 − v 0 ) · (v 1 − v 0 ) × (v 2 − v 0 )を計算することです。領域は、結果と同じ符号を持つ必要があります。
2D 図形の面積比は平行投影では一定であるため、平面に平行ではない単位ベクトル (たとえば z) を選択すると、(v i − v 0 ) × (v i+1 − v 0 )を処理できます。 ·面積としてのz 。これにより、高価な平方根を実行する必要がなくなり、符号チェックが自動的に処理されます。
各三角形の重心は(v 0 + v i + v i+1 ) ÷ 3です。
したがって、ポリゴン全体の重心は、密度が一様であると仮定すると、
1 N-1
centroid = —————————— ∑ ( centroid-of-triangle-i × area-of-triangle-i )
total-area i=1
(寸法 ≥ 4D の場合、面積は A i = ½ |v i −v 0 | |v i+1 −v 0 | sin θ iで計算する必要があります。ここで、cos θ i = (v i −v 0 ) · (v i+1 −v 0 ). )
平面の場合は、平面にローカルな座標系に変換し、提示した式を使用して図心を計算してから、元に戻して3D空間の座標を取得できます。