フィボナッチ数のリストを作成する方法は知っていますが、特定の数がフィボナッチ数のリストに属しているかどうかをテストする方法がわかりません - 頭に浮かぶ 1 つの方法は、フィボナッチ数のリストを生成することです。その数までの数を調べて、それが配列に属しているかどうかを確認しますが、別のより簡単で高速な方法が必要です。
何か案は ？
51713 次
21 に答える
91
5 N^2 + 4非常に優れたテストは、またはが平方数である場合に限り、 N がフィボナッチ数であることです5N^2 – 4。数値が二乗であることを効率的にテストする方法については、SO の議論を参照してください。
お役に立てれば
于 2010-03-12T12:36:26.853 に答える
52
于 2010-03-12T12:36:03.377 に答える
35
完全二乗法を指摘する人もいますが、これにはフィボナッチ数の二乗が含まれるため、多くの場合、巨大な積が得られます。
標準の 64 ビット整数でも保持できるフィボナッチ数は 80 未満です。
これが私の解決策です。これは、テストする数よりも完全に小さく動作します。
(C# で書かれており、doubleやのような基本的な型を使用してlongいます。しかし、アルゴリズムはより大きな型でもうまく機能するはずです。)
static bool IsFib(long T, out long idx)
{
double root5 = Math.Sqrt(5);
double phi = (1 + root5) / 2;
idx = (long)Math.Floor( Math.Log(T*root5) / Math.Log(phi) + 0.5 );
long u = (long)Math.Floor( Math.Pow(phi, idx)/root5 + 0.5);
return (u == T);
}
私がこの回答を書いてから 4 年以上が経過した後、コメント投稿者が 2 番目のパラメーターについて尋ねました
out。
パラメータ #2 は、フィボナッチ数列への「インデックス」です。
テストする値がTフィボナッチ数の場合、idxフィボナッチ数列におけるその数の 1 ベースのインデックスになります。(注目すべき例外が 1 つあります)
フィボナッチ数列は1 1 2 3 5 8 13など
です。3 は数列の 4 番目の数字です。IsFib(3, out idx);戻りtrue値は となります4。
8 はシーケンスの 6 番目の数字です:と valueIsFib(8, out idx);を返します。
13 は 7 番目の数字です。と valueを返します。true6IsFib(13, out idx);true7
1 つの例外はです。値 1 がインデックス 1 と 2 の両方に表示されますがIsFib(1, out idx);、これは を返します。2
IsFibに非フィボナッチ数が渡されると、 が返さfalseれ、 の値は未満idxの最大のフィボナッチ数のインデックスになりTます。
16 はフィボナッチ値ではありません。と valueIsFib(16, out idx);を返します。Binet の公式を
使用して、インデックス 7 を 16 未満の最大数であるフィボナッチ値 13 に変換できます。false7
于 2010-05-12T21:13:55.430 に答える
21
#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
echo "$victim is a fibonacci number"
else
echo "$victim aint"
fi
于 2010-05-12T18:53:54.713 に答える
12
数値のサイズが制限されている場合は、上限を下回るすべてのフィボナッチ数を単純にハッシュテーブルに入れ、封じ込めをテストするだけでうまくいきます。指数関数的に増加するため、フィボナッチ数はほとんどありません (たとえば、5mln 未満の 38 のみ)。
数値のサイズが制限されていない場合、平方テストで提案されたトリックは、数値が見つかるかそれを超えるまで、フィボナッチ数列を生成するよりもほぼ確実に遅くなります。
于 2010-03-12T13:01:22.300 に答える
11
解決に向けて、Binet の公式を見てみましょう。(ウィキペディアのフィボナッチ数
の下にある「閉形式式」を探してください)
フィボナッチ数列は、単純な閉じた式によって作成されると書かれています。
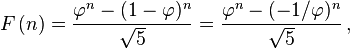
を解いてが整数nかどうかをテストすれば、答えが得られると思います。n
編集@psmears が指摘しているように、同じウィキペディアの記事には、フィボナッチ数の検出に関するセクションもあります。ウィキペディアは優れた情報源です。
于 2010-05-12T18:48:47.847 に答える
11
正の整数 ω はフィボナッチ数です
5ω 2 + 4 と 5ω 2 - 4 のいずれかが完全な正方形である場合にのみ
Alfred Posamentier と Ingmar Lehmann による The (Fabulous) FIBONACCI Numbersより
bool isFibonacci(int w)
{
double X1 = 5 * Math.Pow(w, 2) + 4;
double X2 = 5 * Math.Pow(w, 2) - 4;
long X1_sqrt = (long)Math.Sqrt(X1);
long X2_sqrt = (long)Math.Sqrt(X2);
return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}
1kとの間のフィボナッチ数を出力するスニペット10k。
for (int i = 1000; i < 10000; i++)
{
if (isFibonacci(i))
Console.Write(" "+i);
}
OMG 4つしかありません!!!
他の方法で
from math import *
phi = 1.61803399
sqrt5 = sqrt(5)
def F(n):
return int((phi**n - (1-phi)**n) /sqrt5)
def isFibonacci(z):
return F(int(floor(log(sqrt5*z,phi)+0.5))) == z
print [i for i in range(1000,10000) if isFibonacci(i)]
于 2010-03-12T12:36:31.890 に答える
9
フィボナッチ数に関するウィキペディアの記事の「フィボナッチ数の認識」セクションを参照してください。
于 2010-05-12T18:49:58.860 に答える
6
フィボナッチ数は指数関数的に増加するため、提案する方法はかなり高速です。もう一つはこれ。
于 2010-03-12T12:37:46.343 に答える
3
私と psmears による以前の回答に基づいて、この C# コードを作成しました。
それはゆっくりとステップを経て、明らかに縮小して最適化することができます:
// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
// eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
double root5 = Math.Sqrt(5);
double PSI = (1 + root5) / 2;
// For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number
double a;
a = T*root5;
a = Math.Log(a) / Math.Log(PSI);
a += 0.5;
a = Math.Floor(a);
idx = (Int32)a;
long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);
if (u == T)
{
return true;
}
else
{
idx = 0;
return false;
}
}
テストの結果、これは最初の 69 個のフィボナッチ数では機能しますが、70 番目ではうまくいかないことがわかりました。
F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails
全体として、何らかの BigInt ライブラリを使用している場合を除き、アルゴリズムを実行するよりも、フィボナッチ数の単純なルックアップ テーブルを用意してそれを確認する方がよいでしょう。
最初の 300 の番号のリストは、オンラインですぐに入手できます。
ただし、十分な精度があり、数値表現システムがオーバーフローしない限り、このコードは実行可能なアルゴリズムの概要を示しています。
于 2010-05-12T19:30:13.023 に答える
2
Re: Ahmad のコード - 再帰やポインターのない単純なアプローチで、かなりナイーブですが、非常に巨大な数 (最新のマシンでは数ミリ秒かかる N 番目の fib 数を検証するために約 2N の追加) 以外の計算能力はほとんど必要ありません。最悪の場合）
// 何かが見つかった場合は pos を返し、見つからなかった場合は 0 を返します (C/C++ は任意の値 !=0 を true として扱うため、最終結果は同じです)
int isFib (long n)
{
int pos = 2;
long last = 1;
long current = 1;
long temp;
while (current < n)
{
temp = last;
last = current;
current = current + temp;
pos++;
}
if (current == n)
return pos;
else
return 0;
}
于 2012-05-31T21:13:34.477 に答える
2
ウィキペディアから: http://en.wikipedia.org/wiki/Fibonacci_number
正の整数 z は、5z^2 + 4 または 5z^2 − 4 のいずれかが完全平方である場合にのみ、フィボナッチ数です。
于 2010-05-12T18:52:09.237 に答える
1
フィボナッチ数の一般式は、F(n) = [ [(1+sqrt(5))/2] sup n+1 - [(1-sqrt(5))/2] sup n+1 ]/ sqrt です。 (5) ..... (*) n が大きい場合、2 番目の指数関数はゼロになり、数値演算を実行すると、F(n) = [ (1.618) sup n+1 ] / 2.236 が得られます。
K がテスト対象の数値である場合、log(k*2.2336)/log(1.618) は整数でなければなりません!
K が 13 に等しい場合、私の計算機は答え 7.00246 を返します。K が 14 に等しい場合、答えは 7.1564 です。
答えに最も近い整数を取り、(*) を代入して結果が K であることを確認することで、結果の信頼性を高めることができます。
于 2011-04-04T00:23:17.417 に答える
0
あなたが扱っている数字はどれくらいですか？
ルックアップテーブルはあなたのために働くことができますか？（検索できる番号の事前計算されたリスト）
解析的に答えを得るために反転できると思う閉じた形の式もあります（私は数学者ではないので、この提案が理にかなっているとは約束できません）
于 2010-05-12T18:47:51.280 に答える
0
これは私の解決策であり、ベンチマークかどうかはわかりません。これがお役に立てば幸いです。
def is_fibonacci?(i)
a,b=0,1
until b >= i
a,b=b,a+b
return true if b == i
end
end
a、b = b、a+bが行っていること
0, 1 = 1, 0 +1
1, 1 = 1, 1 + 1
1, 2 = 2, 1 + 2
2, 3 = 3, 2 + 3
fib1 = fib2
fib2 = fib1 + fib2
于 2013-02-22T23:49:40.577 に答える
0
ここで紹介する方法について、単純な加算、配列の事前計算、結果のハッシュへのメモ化を行って、いくつかのベンチマークを実行しました。少なくとも Perl の場合、2 乗法は対数法よりも少し速く、おそらく 20% 高速です。abelenky が指摘しているように、ビット数を 2 乗する余地があるかどうかはトレードオフです。
確かに、最も速い方法は、ドメイン スペース内のすべてのフィボナッチ数をハッシュすることです。abelenky が指摘するもう 1 つの点に沿って、2^64 未満の吸盤は 94 個しかありません。
それらを事前に計算して、Perl ハッシュ、Python 辞書などに入れる必要があります。
フィボナッチ数の性質は非常に興味深いものですが、それを使用してコンピューター プログラム内の整数が 1 かどうかを判断することは、プログラムが起動するたびに pi を計算するサブルーチンを作成するようなものです。
于 2010-05-12T22:19:24.203 に答える
0
基本的にすべての回答が与えられます。非常に高速な C++ のサンプル コードを追加したいと思います。
基礎となるのは、ここですでに何度か言及されているルックアップ メカニズムです。
Binet の式を使用すると、2021 年現在、通常 64 ビットの C++ データ型に適合するフィボナッチ数は非常に少ないと計算できますunsigned long long。ラウンドアバウト 93 です。これは、今日では非常に低い数です。
最新の C++ 17 (およびそれ以降) の機能を使用すると、コンパイル時std::arrayに 64 ビット データ型のすべてのフィボナッチ数を簡単に作成できます。
したがって、93*8= 744バイトの非ランタイム メモリをルックアップ配列に使用します。
そしてstd::binary_search、値を見つけるために使用します。したがって、関数全体は次のようになります。
bool isFib(const unsigned long long numberToBeChecked) {
return std::binary_search(FIB.begin(), FIB.end(), numberToBeChecked);
}
FIB はコンパイル時間ですconstexpr std::array。では、その配列を構築する方法は?
最初に、フィボナッチ数をconstexpr関数として計算するためのデフォルトのアプローチを定義します。
// Constexpr function to calculate the nth Fibonacci number
constexpr unsigned long long getFibonacciNumber(size_t index) noexcept {
// Initialize first two even numbers
unsigned long long f1{ 0 }, f2{ 1 };
// Calculating Fibonacci value
while (index--) {
// get next value of Fibonacci sequence
unsigned long long f3 = f2 + f1;
// Move to next number
f1 = f2;
f2 = f3;
}
return f2;
}
これにより、実行時にフィボナッチ数を簡単に計算できます。std::array次に、すべてのフィボナッチ数でa を埋めます。も使用constexprし、可変引数パックを使用してテンプレートにします。
std::integer_sequenceインデックス 0,1,2,3,4,5, ... のフィボナッチ数を作成するために使用します。
これは簡単で複雑ではありません。
template <size_t... ManyIndices>
constexpr auto generateArrayHelper(std::integer_sequence<size_t, ManyIndices...>) noexcept {
return std::array<unsigned long long, sizeof...(ManyIndices)>{ { getFibonacciNumber(ManyIndices)... } };
};
この関数には整数シーケンス 0,1,2,3,4,... が与えられstd::array<unsigned long long, ...>、対応するフィボナッチ数とともに a が返されます。
最大 93 個の値を格納できることがわかっています。したがって、整数シーケンス 1,2,3,4,...,92,93 を使用して上記を呼び出す次の関数を作成します。次のようになります。
constexpr auto generateArray() noexcept {
return generateArrayHelper(std::make_integer_sequence<size_t, MaxIndexFor64BitValue>());
}
そして今、最後に、
constexpr auto FIB = generateArray();
std::array<unsigned long long, 93>すべてのフィボナッチ数を含む FIB という名前のコンパイル時が得られます。i 番目のフィボナッチ数が必要な場合は、単純に と書くことができますFIB[i]。実行時の計算はありません。
サンプルプログラム全体は次のようになります。
#include <iostream>
#include <array>
#include <utility>
#include <algorithm>
#include <iomanip>
// ----------------------------------------------------------------------
// All the following will be done during compile time
// Constexpr function to calculate the nth Fibonacci number
constexpr unsigned long long getFibonacciNumber(size_t index) noexcept {
// Initialize first two even numbers
unsigned long long f1{ 0 }, f2{ 1 };
// calculating Fibonacci value
while (index--) {
// get next value of Fibonacci sequence
unsigned long long f3 = f2 + f1;
// Move to next number
f1 = f2;
f2 = f3;
}
return f2;
}
// We will automatically build an array of Fibonacci numbers at compile time
// Generate a std::array with n elements
template <size_t... ManyIndices>
constexpr auto generateArrayHelper(std::integer_sequence<size_t, ManyIndices...>) noexcept {
return std::array<unsigned long long, sizeof...(ManyIndices)>{ { getFibonacciNumber(ManyIndices)... } };
};
// Max index for Fibonaccis that for an 64bit unsigned value (Binet's formula)
constexpr size_t MaxIndexFor64BitValue = 93;
// Generate the required number of elements
constexpr auto generateArray()noexcept {
return generateArrayHelper(std::make_integer_sequence<size_t, MaxIndexFor64BitValue>());
}
// This is an constexpr array of all Fibonacci numbers
constexpr auto FIB = generateArray();
// All the above was compile time
// ----------------------------------------------------------------------
// Check, if a number belongs to the Fibonacci series
bool isFib(const unsigned long long numberToBeChecked) {
return std::binary_search(FIB.begin(), FIB.end(), numberToBeChecked);
}
// Test
int main() {
const unsigned long long testValue{ 498454011879264ull };
std::cout << std::boolalpha << "Does '" <<testValue << "' belong to Fibonacci series? --> " << isFib(498454011879264) << '\n';
return 0;
}
Microsoft Visual Studio Community 2019、バージョン 16.8.2 で開発およびテスト済み
さらに、gcc 10.2 および clang 11.0.1 でテスト済み
言語: C++ 17
于 2021-01-30T09:41:34.510 に答える
0
Java ソリューションは、以下のように実行できます。しかし、それでも最適化することができます
次のソリューションは
- 1≦T≦10 ^5
- 1≦N≦10 ^10
T はテスト ケースの数、N は数の範囲
import java.util.Scanner;
import java.math.BigDecimal;
import java.math.RoundingMode;
public class FibonacciTester {
private static BigDecimal zero = BigDecimal.valueOf(0);
private static BigDecimal one = BigDecimal.valueOf(1);
private static BigDecimal two = BigDecimal.valueOf(2);
private static BigDecimal four = BigDecimal.valueOf(4);
private static BigDecimal five = BigDecimal.valueOf(5);
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
BigDecimal[] inputs = new BigDecimal[n];
for (int i = 0; i < n; i++) {
inputs[i] = sc.nextBigDecimal();
}
for (int i = 0; i < inputs.length; i++) {
if (isFibonacci(inputs[i]))
System.out.println("IsFibo");
else
System.out.println("IsNotFibo");
}
}
public static boolean isFibonacci(BigDecimal num) {
if (num.compareTo(zero) <= 0) {
return false;
}
BigDecimal base = num.multiply(num).multiply(five);
BigDecimal possibility1 = base.add(four);
BigDecimal possibility2 = base.subtract(four);
return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
}
public static boolean isPerfectSquare(BigDecimal num) {
BigDecimal squareRoot = one;
BigDecimal square = one;
BigDecimal i = one;
BigDecimal newSquareRoot;
int comparison = -1;
while (comparison != 0) {
if (comparison < 0) {
i = i.multiply(two);
newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
} else {
i = i.divide(two);
newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
}
if (newSquareRoot.compareTo(squareRoot) == 0) {
return false;
}
squareRoot = newSquareRoot;
square = squareRoot.multiply(squareRoot);
comparison = square.compareTo(num);
}
return true;
}
}
于 2014-12-31T06:46:09.740 に答える
-1
int isfib(int n /* number */, int &pos /* position */)
{
if (n == 1)
{
pos=2; // 1 1
return 1;
}
else if (n == 2)
{
pos=3; // 1 1 2
return 1;
}
else
{
int m = n /2;
int p, q, x, y;
int t1=0, t2 =0;
for (int i = m; i < n; i++)
{
p = i;
q = n -p; // p + q = n
t1 = isfib(p, x);
if (t1) t2 = isfib(q, y);
if (t1 && t2 && x == y +1)
{
pos = x+1;
return 1; //true
}
}
pos = -1;
return 0; //false
}
}
これはどう？
于 2011-11-22T18:58:03.700 に答える
-1
#include <stdio.h>
#include <math.h>
int main()
{
int number_entered, x, y;
printf("Please enter a number.\n");
scanf("%d", &number_entered);
x = y = 5 * number_entered^2 + 4; /*Test if 5N^2 + 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
printf("That number is in the Fibonacci sequence.\n");
}
x = y = 5 * number_entered^2 - 4; /*Test if 5N^2 - 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
printf("That number is in the Fibonacci sequence.\n");
}
else
{
printf("That number isn't in the Fibonacci sequence.\n");
}
return 0;
}
これは機能しますか？
于 2012-07-22T11:33:40.650 に答える