11 
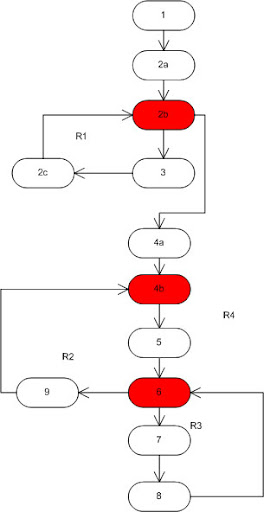
insertion_procedure (int a[], int p [], int N)
{
    int i,j,k;
    for (i=0; i<=N; i++) p[i] = i;
    for (i=2; i<=N; i++)
    {
        k = p[i];
        j = 1;
        while (a[p[j-1]] > a[k]) {p[j] = p[j-1]; j--}
        p[j] = k;
    }
}

このコードの循環的複雑度を見つけて、いくつかのホワイト ボックス テスト ケースとブラック ボックス テスト ケースを提案する必要があります。しかし、コードの CFG を作成するのに問題があります。

テストケースについても助けていただければ幸いです。

4

3 に答える 3

28

ステートメントに番号を付けることから始めます。

 insertion_procedure (int a[], int p [], int N)
 {
(1)    Int i,j,k;
(2)    for ((2a)i=0; (2b)i<=N; (2c)i++) 
(3)        p[i] = i;
(4)    for ((4a)i=2; (4b)i<=N; (4c)i++)
       {
(5)       k=p[i];j=1;
(6)       while (a[p[j-1]] > a[k]) {
(7)           p[j] = p[j-1]; 
(8)           j--
          }
(9)          p[j] = k;
       }

これで、どのステートメントが最初に実行され、どのステートメントが最後に実行されるかなどを明確に確認できるため、cfg の描画が簡単になります。

CFG

ここで、循環的複雑度を計算するには、次の 3 つの方法のいずれかを使用します。

  1. グラフ上の領域の数を数えます: 4
  2. 述語の数 (グラフの赤) + 1 : 3 + 1 = 4
  3. エッジの数 - いいえ。ノード数 + 2: 14 - 12 + 2 = 4.
于 2010-04-19T19:21:12.330 に答える
3

循環的複雑度は 4 です。

プロシージャの場合は 1 + for ループの場合は +1 while ループの場合は +1 while ループの if 条件の場合は 1。

于 2010-04-19T18:58:00.453 に答える
2

McCabe 式を使用することもできますM = E-N + 2C
E = エッジ
N = ノード
C = コンポーネント
M = 循環的複雑度

E = 14
N = 12
C = 1

M = 14-12 + 2*1 = 4

于 2011-12-06T23:15:09.120 に答える