3

私はこのように書かれた数学の問題を抱えています：

x^1+x^2+x^3+...+x^n

これらの種類の方程式を解くのに役立つC＃の構造はありますか？

これを実現するためにforループを記述したり、再帰を使用したりできることは知っていますが、後で実行するためにそのようなステートメントをプリコンパイルするc＃の構造について読んだことを覚えています。

これらの種類の方程式を解くための興味深い方法はありますか？

4

6 に答える 6

8

x^n を計算するには、Math.Powを使用します。

Math.Pow(x, n)

合計を計算する場合は、ループまたは LINQ を使用できます。ここでは単純なループに問題はないと思います。

double total = 0;
for (int i = 1; i <= n; ++i)
{
    total += Math.Pow(x, i);
}
Console.WriteLine(total);

これは LINQ で記述できますが、そうする特に強い理由はありません。おそらく、探している機能を拡張できますか? より良いパフォーマンスをお探しですか？

あなたの質問には「数学的最適化」というタグが付けられているため、ショートカットを見つけて最適化することもできます。この特定のケースでは、幾何級数であるため、次の式を使用できます。

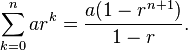
代替テキスト

または C# の場合:

static double geometricSeries(double a, double r, int n)
{
    return a * (1 - Math.Pow(r, n + 1)) / (1 - r);
}

他のより複雑なケースでは、式を見つけるのがより困難になる場合があります。

于 2010-08-14T19:37:41.230 に答える
7

あなたの例は意図的に些細なことだと理解しています。ただし、実際に計算しようとしているものが依然として多項式である場合は、間違いなくホーナー スキームを使用する必要があります。これが C# の実装です。

于 2010-08-14T19:57:34.223 に答える
5

遅延実行にデリゲートを使用することについて話しているかもしれません。しかし多くの場合、それはメソッドを書くことと同じです。たとえば、「簡単な」方法から始めましょう。

public static double SumExponents(double x, int n)
{
    double total = 0;
    for (int i = 1; i <= n; i++)
    {
         total += Math.Pow(x, i);
    }
    return total;
}

これは、LINQ を使用して次のように記述できます。

public static double SumExponents(double x, int n)
{
    return Enumerable.Range(1, n)
                     .Select(i => Math.Pow(x, i))
                     .Sum();
}

次に、これを単一のラムダ式として記述できます。

Func<double, int, double> func = (x, n) => Enumerable.Range(1, n)
                                              .Select(i => Math.Pow(x, i))
                                              .Sum();

そういうことを考えていたのですか？そうでない場合は、質問を明確にしてください。あなたが探しているものは本当に明白ではありません。

于 2010-08-14T19:39:33.413 に答える
1

等比数列について C# に固有のものはありません。この合計は O(1) 時間で計算できます。（電源操作には一定の時間がかかると仮定します。）

あなたの場合、式は次のようになります

x*(x^n - 1)/(x - 1)
于 2010-08-14T19:42:17.027 に答える
0 
int total = 0;
for(int i = 1; i <= n; i++)
    total += Math.Pow(x, i);
于 2010-08-14T19:38:47.717 に答える
0

Aggregateselect\sum だけでなく、折り畳みシーケンスにも使用できます。

int n;
double x;
double result = Enumerable.Range(1, n)
    .Aggregate(0.0, (acc, i) => acc + Math.Pow(x, i));
于 2010-08-14T19:46:39.853 に答える