3

(-x または 0) -> 無限大からの積分について、MATLABquadgkと Python のルーチンの間で一貫性のない結果が得られます。quadMATLAB バージョンは (パラメーターを 1 から -1 に切り替えるセンス チェックに基づいて) 正しいと思いますがflag、Python バージョンは誤った結果 (この場合は 0) を返します。MATLAB は 0.1022 を生成します。これらintegrandsは同一であり、xMATLAB によって生成された値quadgkを Python に挿入することも含め、各ステップを結び付けました (その結果、Python バージョンは MATLAB と同じ値を生成し、それらをintegrand関数に渡すだけです)。この時点で、SciPy ではなく、Gauss-Legendre 求積法 ( https://sourceforge.net/projects/fastgausslegendrequadrature/ ) などの別のルーチンを使用することを検討しています。しかし、それを a/b 範囲から -a->infinity に拡張する方法がわかりません (有限数にしか到達しないこれらの方法を見てきました:

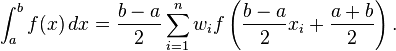https://upload.wikimedia.org/math/a/7/f/ numpy での Gauss-Legendre 求積の間隔が異なるのに対し、b=np.Inf結果はNaN. また、変換を読んでいますが、返されたノードと重みから統合をセットアップする方法もわかりませんが、 a と b の有限範囲のみです: https://pomax.github.io/bezierinfo/legendre-gauss.htmlどちらかそれまたは誰かがこれを処理できる Python ライブラリを知っている場合 - quad600,000 個の関数をすばやく統合する必要があるため (つまり、C++ ライブラリへのリンク上記リンク）。ここで本当に奇妙なのは、上に移動して同じ結果を得ることができたことです。volPython の結果は 0 で崩壊します。非常に紛らわしいです。微積分から何年も経ちました...ここにPythonコードがあります：

from scipy.stats import norm, lognorm
from scipy.integrate import quad
import numpy as np

def integrand(x, flag, F, K, vol, T2, T1):
    d1 = (np.log(x / (x+K)) + 0.5 * (vol**2) * (T2-T1)) / (vol * np.sqrt(T2 - T1))
    d2 = d1 - vol*np.sqrt(T2 - T1)
    mu = np.log(F) - 0.5 *vol **2 * T1
    sigma = vol * np.sqrt(T1)
    value = lognorm.pdf(x, scale=np.exp(mu), s=sigma) * (flag * x*norm.cdf(flag * d1) - flag * (x+K)*norm.cdf(flag * d2))
    return value

if __name__ == '__main__':
        flag = 1
        F = 54.31
        K = 1.1967
        vol = 0.1328
        T2 = 0.0411
        T1 = 0.0137
        quad(integrand, 0, np.Inf, args=(flag, F, K, vol, T2, T1), epsabs=1e-12)[0]

MATLAB コードは次のとおりです ( integrand.M として保存する必要があり、コマンド ウィンドウにスクリプトを入力できます)。

function value = integrand(x, flag, F,K,vol,T2,T1)
d1 = (log(x ./ (x+K)) + 0.5 .* (vol.^2) .* (T2-T1)) ./ (vol .* sqrt(T2 - T1));
d2 = d1 - vol.*sqrt(T2 - T1);
mu = log(F) - 0.5 .*vol .^2 .* T1;
sigma = vol .* sqrt(T1);
value = lognpdf(x, mu, sigma) .* (flag .* x.*normcdf(flag .* d1) - flag .* (x+K).*normcdf(flag .* d2));
end

% スクリプト部分

flag = 1
F = 54.31
K = 1.1967
vol = 0.1328
T2 = 0.0411
T1 = 0.0137
quadgk(@(x) integrand(x,flag, F, K, vol, T2, T1), 0, Inf, 'AbsTol',1e-12)

MATLAB と Python は、代わりにこれらの入力が渡された場合 (変数の上で転置)、クワッドを使用して同じ結果を生成することに注意してください。

 current_opt = [  -1.0000    1.2075    0.1251    0.4300    0.0685    0.0411     
                1.0000    1.2075    0.0512    0.5600    0.0685    0.0411]
4

1 に答える 1

0

これは面白いですね。epsabs変数が途方もなく高く設定されない限り、統合は崩壊します。を使用して、MATLAB と Python の間で結果を複製することができましたepsabs=-1e1000。できる限り遅くなりますが、少なくとも機能します。

于 2016-05-21T18:34:57.950 に答える