さらに処理する前に外れ値を削除するために、データセットのおおよそのパーセンタイル(順序統計量)を繰り返し計算する必要があるプログラムがあります。私は現在、値の配列を並べ替えて適切な要素を選択することでこれを行っています。これは実行可能ですが、プログラムのかなりマイナーな部分であるにもかかわらず、プロファイルの目立ったブリップです。
より詳しい情報:
- データセットには最大100000の浮動小数点数が含まれ、「合理的に」分散されていると想定されます。特定の値の近くで密度が重複したり、大きなスパイクが発生したりする可能性はほとんどありません。また、何らかの奇妙な理由で分布が奇妙な場合は、データがとにかく混乱し、さらに処理が疑わしいため、近似の精度が低くても問題ありません。ただし、データは必ずしも均一または正規分布しているとは限りません。退化する可能性は非常に低いです。
- 近似解は問題ありませんが、それが有効であることを確認するには、近似がどのようにエラーを引き起こすかを理解する必要があります。
- 外れ値を削除することが目的なので、常に同じデータに対して2つのパーセンタイルを計算しています。たとえば、1つは95%、もう1つは5%です。
- アプリはC#であり、C++では少し手間がかかります。擬似コードまたはいずれかの既存のライブラリで問題ありません。
- 外れ値を削除するまったく異なる方法も、合理的である限り問題ありません。
- 更新:おおよその選択アルゴリズムを探しているようです。
これはすべてループで実行されますが、データは毎回(わずかに)異なるため、この質問で行ったようにデータ構造を再利用するのは簡単ではありません。
実装されたソリューション
Gronimが提案したウィキペディア選択アルゴリズムを使用すると、実行時間のこの部分が約20分の1に短縮されました。
C#の実装が見つからなかったので、これが私が思いついたものです。Array.Sortよりも小さな入力でも高速です。そして1000要素でそれは25倍速くなります。
public static double QuickSelect(double[] list, int k) {
return QuickSelect(list, k, 0, list.Length);
}
public static double QuickSelect(double[] list, int k, int startI, int endI) {
while (true) {
// Assume startI <= k < endI
int pivotI = (startI + endI) / 2; //arbitrary, but good if sorted
int splitI = partition(list, startI, endI, pivotI);
if (k < splitI)
endI = splitI;
else if (k > splitI)
startI = splitI + 1;
else //if (k == splitI)
return list[k];
}
//when this returns, all elements of list[i] <= list[k] iif i <= k
}
static int partition(double[] list, int startI, int endI, int pivotI) {
double pivotValue = list[pivotI];
list[pivotI] = list[startI];
list[startI] = pivotValue;
int storeI = startI + 1;//no need to store @ pivot item, it's good already.
//Invariant: startI < storeI <= endI
while (storeI < endI && list[storeI] <= pivotValue) ++storeI; //fast if sorted
//now storeI == endI || list[storeI] > pivotValue
//so elem @storeI is either irrelevant or too large.
for (int i = storeI + 1; i < endI; ++i)
if (list[i] <= pivotValue) {
list.swap_elems(i, storeI);
++storeI;
}
int newPivotI = storeI - 1;
list[startI] = list[newPivotI];
list[newPivotI] = pivotValue;
//now [startI, newPivotI] are <= to pivotValue && list[newPivotI] == pivotValue.
return newPivotI;
}
static void swap_elems(this double[] list, int i, int j) {
double tmp = list[i];
list[i] = list[j];
list[j] = tmp;
}
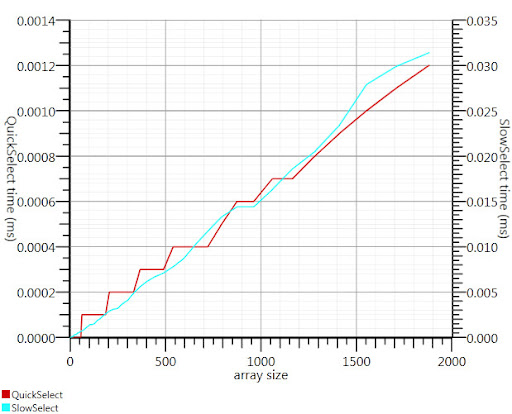
グロニム、私を正しい方向に向けてくれてありがとう!