3

matlab FAQ では、極大値を見つけるための 1 行の方法について説明しています。

index = find( diff( sign( diff([0; x(:); 0]) ) ) < 0 );

しかし、これはデータが多かれ少なかれ滑らかな場合にのみ機能すると思います。小さな間隔で上下にジャンプするデータがあるが、それでも近似的な極大値がいくつかあるとします。これらのポイントを見つけるにはどうすればよいでしょうか。ベクトルを n 個に分割し、それぞれの端にない最大値を見つけることができますが、よりエレガントで高速なソリューションがあるはずです。

1行のソリューションも素晴らしいでしょう。

編集:私はノイズの多い生物学的画像を扱っており、それを個別のセクションに分割しようとしています。

4

4 に答える 4

3

処理しているデータの種類はわかりませんが、音声データの処理に使用した方法で、極大値を見つけるのに役立ちます。信号処理ツールボックスの3つの関数、HILBERT、BUTTER、およびFILTFILTを使用します。

data = (...the waveform of noisy data...);
Fs = (...the sampling rate of the data...);
[b,a] = butter(5,20/(Fs/2),'low');  % Create a low-pass butterworth filter;
                                    %   adjust the values as needed.
smoothData = filtfilt(b,a,abs(hilbert(data)));  % Apply a hilbert transform
                                                %   and filter the data.

次に、 smoothDataで最大値の検索を実行します。HILBERTを使用すると、最初にデータに正のエンベロープが作成され、次にFILTFILTがBUTTERのフィルター係数を使用してデータエンベロープをローパスフィルター処理します。

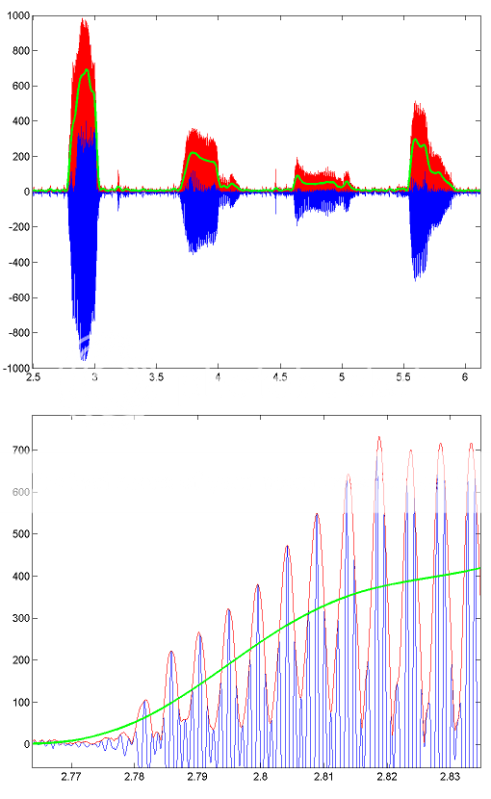
この処理がどのように機能するかの例として、録音された音声のセグメントの結果を示すいくつかの画像があります。青い線は元の音声信号、赤い線はエンベロープ（HILBERTを使用して取得）、緑の線はローパスフィルター処理された結果です。下の図は、最初の拡大版です。

代替テキスト

試してみるランダム：

これは私が最初に思いついたランダムなアイデアでした...最大値の最大値を見つけることによってプロセスを繰り返すことを試みることができます：

index = find(diff(sign(diff([0; x(:); 0]))) < 0);
maxIndex = index(find(diff(sign(diff([0; x(index); 0]))) < 0));

ただし、信号対雑音比によっては、関心のある極大値を取得するためにこれを何回繰り返す必要があるかは不明です。これは、ランダムな非フィルタリングオプションです。=）

マキシマファインディング：

念のために言っておきますが、私が見たもう1つの1行の最大値検出アルゴリズム（リストしたものに加えて）は次のとおりです。

index = find((x > [x(1) x(1:(end-1))]) & (x >= [x(2:end) x(end)]));
于 2009-05-08T23:03:52.090 に答える
2

必要に応じて、ノイズの多いデータをフィルター処理すると役立つことがよくあります。MEDFILT1を見るか、FSPECIALとともにCONVを使用してください。後者のアプローチでは、CONV に「同じ」引数を使用し、FSPECIAL によって作成された「ガウス」フィルターを使用することをお勧めします。

フィルタリングを行った後、最大値ファインダーにフィードします。

編集: ランタイムの複雑さ

入力ベクトルの長さが X で、フィルター カーネルの長さが K であるとします。

メジアン フィルターは実行中の挿入ソートを実行することで機能するため、O(X K + K log K)になるはずです。ソースコードは見ていませんし、他の実装も可能ですが、基本的には O(X K)のはずです。

K が小さい場合、conv は単純な O(X*K) アルゴリズムを使用します。X と K がほぼ同じ場合、高速フーリエ変換を使用する方が高速です。その実装は O(X log X + K log K) です。Matlab は、入力サイズに応じて適切なアルゴリズムを自動的に選択するほどスマートです。

于 2009-05-09T02:08:15.813 に答える
1

データが大幅に上下する場合、関数には多くの極大値があります。だから私はあなたがすべての極大を見つけたくないと仮定しています。しかし、極大値が何であるかについてのあなたの基準は何ですか？基準がある場合は、そのためのスキームまたはアルゴリズムを設計できます。

今のところ、最初にローパスフィルターをデータに適用してから、極大値を見つける必要があると思います。フィルタリング後の極大値の位置は、前の位置と正確に一致しない場合がありますが。

于 2009-05-08T23:05:57.483 に答える
1

このような問題を表示するには、2 つの方法があります。これは主に、フィルタリング ツールを使用してデータを平滑化した後、補間スプラインなどのさまざまな補間関数を使用して補間する平滑化の問題と見なすことができます。補間スプラインの極大値を見つけるのは簡単なことです。(一般に、ここでは pchip 内挿ではなく、真のスプラインを使用する必要があることに注意してください。interp1 で「3 次」内挿を指定するときに使用される方法である Pchip では、2 つのデータ ポイントの間にあるローカル ミニマイザーを正確に特定できません。)

このような問題に対するもう 1 つのアプローチは、私が好んで使用するアプローチです。ここでは、最小二乗スプライン モデルを使用して、データを平滑化し、内挿ではなく近似を生成します。このような最小二乗スプラインには、問題に関する知識をモデルに導入するために、ユーザーが大幅に制御できるという利点があります。たとえば、科学者やエンジニアは、研究中のプロセスに関する単調性などの情報を持っていることがよくあります。これは、最小二乗スプライン モデルに組み込むことができます。もう 1 つの関連するオプションは、平滑化スプラインを使用することです。それらも、組み込みの正則化制約を使用して構築できます。スプライン ツールボックスがある場合、spap2 はスプライン モデルに適合するためのユーティリティになります。次に、fnmin は最小化ツールを見つけます。(マキシマイザーは、最小化コードから簡単に取得できます。)

フィルタリング方法を使用する平滑化スキームは、一般に、データ ポイントが等間隔である場合に最も単純になります。不等間隔は、最小二乗スプライン モデルを推し進める可能性があります。一方、最小二乗スプラインではノットの配置が問題になる場合があります。このすべての私のポイントは、どちらのアプローチにもメリットがあり、実行可能な結果を​​生み出すことができることを示唆することです.

于 2009-05-09T03:52:59.977 に答える