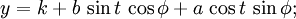楕円の長軸が垂直または水平の場合、バウンディング ボックスを計算するのは簡単ですが、楕円を回転させた場合はどうでしょうか。
これまでに考えられる唯一の方法は、周囲のすべてのポイントを計算し、最大/最小の x および y 値を見つけることです。もっと簡単な方法があるはずです。
任意の角度で楕円を記述する関数 (数学的な意味で) がある場合、その導関数を使用して、勾配がゼロまたは未定義の点を見つけることができますが、見つけることができないようです。
編集：明確にするために、軸に沿ったバウンディングボックスが必要です。つまり、楕円で回転するのではなく、x軸に合わせたままにする必要があるため、バウンディングボックスの変換は機能しません。
任意の角度で回転した楕円に対してパラメータ化された方程式を使用してみることができます。
x = h + a*cos(t)*cos(phi) - b*sin(t)*sin(phi) [1]
y = k + b*sin(t)*cos(phi) + a*cos(t)*sin(phi) [2]
...ここで、楕円は中心 (h,k) の長半径 a と短半径 b を持ち、角度 phi だけ回転します。
次に、勾配 = 0 を微分して解くことができます。
0 = dx/dt = -a*sin(t)*cos(phi) - b*cos(t)*sin(phi)
=>
tan(t) = -b*tan(phi)/a [3]
これにより、t の多くのソリューションが得られます (そのうちの 2 つに興味があります)。それを [1] に戻して、最大 x と最小 x を取得します。
[2] について繰り返します。
0 = dy/dt = b*cos(t)*cos(phi) - a*sin(t)*sin(phi)
=>
tan(t) = b*cot(phi)/a [4]
例を試してみましょう：
(0,0) で a=2、b=1 の楕円を PI/4 で回転させたものを考えてみましょう。
[1] =>
x = 2*cos(t)*cos(PI/4) - sin(t)*sin(PI/4)
[3] =>
tan(t) = -tan(PI/4)/2 = -1/2
=>
t = -0.4636 + n*PI
t = -0.4636 と t = -3.6052 に関心があります。
したがって、次のようになります。
x = 2*cos(-0.4636)*cos(PI/4) - sin(-0.4636)*sin(PI/4) = 1.5811
と
x = 2*cos(-3.6052)*cos(PI/4) - sin(-3.6052)*sin(PI/4) = -1.5811
http://www.iquilezles.org/www/articles/ellipses/ellipses.htmで簡単な式を見つけました(z 軸は無視しました)。
大まかに次のように実装しました。
num ux = ellipse.r1 * cos(ellipse.phi);
num uy = ellipse.r1 * sin(ellipse.phi);
num vx = ellipse.r2 * cos(ellipse.phi+PI/2);
num vy = ellipse.r2 * sin(ellipse.phi+PI/2);
num bbox_halfwidth = sqrt(ux*ux + vx*vx);
num bbox_halfheight = sqrt(uy*uy + vy*vy);
Point bbox_ul_corner = new Point(ellipse.center.x - bbox_halfwidth,
ellipse.center.y - bbox_halfheight);
Point bbox_br_corner = new Point(ellipse.center.x + bbox_halfwidth,
ellipse.center.y + bbox_halfheight);
これは比較的単純ですが、楕円を表現する方法を指定していないため、説明するのが少し難しいです。それを行う方法はたくさんあります。
とにかく、一般的な原則は次のようになります。軸に揃えられた境界ボックスを直接計算することはできません。ただし、xとyの楕円の極値を2D空間の点として計算できます。
このためには、方程式x（t）= ellipse_equation（t）およびy（t）= ellipse_equation（t）を取るだけで十分です。それの1次導関数を取得し、それをルートとして解きます。三角法に基づく楕円を扱っているので、簡単です。最終的に、atan、acos、またはasinを介して根を取得する方程式が得られるはずです。
ヒント：コードを確認するには、回転していない楕円で試してください。ルートは0、Pi / 2、Pi、および3 * Pi/2である必要があります。
各軸（xとy）に対してこれを行います。最大で4つのルートを取得します（楕円が縮退している場合、たとえば半径の1つがゼロの場合はそれより少なくなります）。根元の位置を評価すると、楕円のすべての極値が得られます。
今、あなたはほとんどそこにいます。楕円の境界ボックスを取得するのは、これらの4つのポイントでxmin、xmax、ymin、ymaxをスキャンするのと同じくらい簡単です。
ところで-楕円の方程式を見つけるのに問題がある場合：中心、2つの半径、および中心の周りの回転角を持つ軸整列楕円がある場合にそれを減らすようにしてください。
そうすると、方程式は次のようになります。
// the ellipse unrotated:
temp_x(t) = radius.x * cos(t);
temp_y(t) = radius.y * sin(t);
// the ellipse with rotation applied:
x(t) = temp_x(t) * cos(angle) - temp_y(t) * sin(angle) + center.x;
y(t) = temp_x(t) * sin(angle) + temp_y(t) * cos(angle) + center.y;
最も便利な式はこれだと思います。原点からファイの角度から回転した省略記号は、次の式で表されます。
ここで、（h、k）は中心、aとbは長軸と短軸のサイズで、tは-piからpiまで変化します。
それから、t dx/dtまたはdy/dtが0になるものを導き出すことができるはずです。
楕円がその焦点と離心率によって与えられる場合の式を次に示します(軸の長さ、中心、角度によって与えられる場合については、user1789690 による回答などを参照してください)。
つまり、焦点が (x0, y0) と (x1, y1) で、離心率が e の場合、
bbox_halfwidth = sqrt(k2*dx2 + (k2-1)*dy2)/2
bbox_halfheight = sqrt((k2-1)*dx2 + k2*dy2)/2
どこ
dx = x1-x0
dy = y1-y0
dx2 = dx*dx
dy2 = dy*dy
k2 = 1.0/(e*e)
user1789690 と Johan Nilsson の回答から数式を導き出しました。
これは、任意の向きで楕円にぴったり合う長方形を見つけるための私の関数です
私はopencv rectと実装のポイントを持っています:
cg - 楕円の中心
size - 楕円の長軸、短軸
angle - 楕円の向き
cv::Rect ellipse_bounding_box(const cv::Point2f &cg, const cv::Size2f &size, const float angle) {
float a = size.width / 2;
float b = size.height / 2;
cv::Point pts[4];
float phi = angle * (CV_PI / 180);
float tan_angle = tan(phi);
float t = atan((-b*tan_angle) / a);
float x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
float y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
pts[0] = cv::Point(cvRound(x), cvRound(y));
t = atan((b*(1 / tan(phi))) / a);
x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
pts[1] = cv::Point(cvRound(x), cvRound(y));
phi += CV_PI;
tan_angle = tan(phi);
t = atan((-b*tan_angle) / a);
x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
pts[2] = cv::Point(cvRound(x), cvRound(y));
t = atan((b*(1 / tan(phi))) / a);
x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
pts[3] = cv::Point(cvRound(x), cvRound(y));
long left = 0xfffffff, top = 0xfffffff, right = 0, bottom = 0;
for (int i = 0; i < 4; i++) {
left = left < pts[i].x ? left : pts[i].x;
top = top < pts[i].y ? top : pts[i].y;
right = right > pts[i].x ? right : pts[i].x;
bottom = bottom > pts[i].y ? bottom : pts[i].y;
}
cv::Rect fit_rect(left, top, (right - left) + 1, (bottom - top) + 1);
return fit_rect;
}