問題タブ [computational-geometry]

List1には多数 (~7^10) の N 次元ポイント (N <=10) が含まれ、List2には N 次元ポイント (N <=10)と同数またはそれ以下の数が含まれます。

私の仕事は次のとおりです: List1 のすべての点について、List2 のどの点が List1 の点に最も近いか (ユークリッド距離) を確認し、その後、いくつかの操作を実行したいと考えています。List1 に 50 個を超えるポイントがなかったときはネストされたループの方法で単純に実行してきましたが、7^10 ポイントの場合、明らかに多くの時間がかかります。

これを行う最速の方法は何ですか? 計算幾何学の概念は役に立ちますか?

編集: 私は次の場所にいます。List2から kd ツリーを構築し、 List1の各ポイントに対して最近傍検索を実行しています。最初に指摘したように、List1には 7^10 のポイントがあるため、すべてのペアに対してブルート フォース (ユークリッド距離法) を節約していますが、 List1の膨大な数のポイントが多くの時間を消費しています。これを改善する方法はありますか？

交差光線と三角形をテストするにはどうすればよいですか? また、存在する場合、光線の原点から交点までの距離を取得する方法を教えてください。私のプログラムで、1 つの光線から最大 10000 の三角形をチェックする必要がある場合、どのような最適化を使用できますか??

私は、地図上の特定のポイントを検索するコードを少し書き込もうとしていますが、コンパス方位の特定の弧内にあります。

たとえば、45 度 (北東)、両側 20 度です。

これまでのところ、特定の半径で結果を得る SQL コマンドを取得しました。方向にフィルターする方法について助けが必要です。

これを（可能であれば）すべてSQLで実行できますか、それともPHPを少し適用する必要がありますか？

ありとあらゆる助けが大歓迎です！

次のようなポリゴンチェーンがあります...

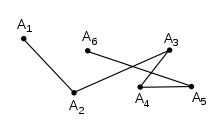
...画像にチェーンがある場合、パスを交差させずに同じ形状を定義するチェーンを計算するにはどうすればよいですか？

具体的には、画像の入力チェーンの場合、必要な結果は次のようになります。

A1、
A2、A2とA3の
交差 、A3とA4の 交差、A4、A5、A3とA4の交差、A3、A3とA2 の交差、A6

あらゆるチェーンでこれを実現するアルゴリズムを探していますが、何をしようとしているのかわからないため、解決策を探すのは難しいです。

私がやろうとしていることの名前があれば、それを知ることは大いに役立つでしょう。

助けてくれてありがとう！

I 2セットのk次元ベクトル。ここで、kは約500で、ベクトルの数は通常これより少なくなります。2つのセット間の（任意に定義された）最小距離を計算したいと思います。素朴なアプローチはこれです：

ただし、これにはO（n²*距離）の計算が必要です。これを行うより速い方法はありますか？

単純な（穴や自己交差のない）ポリゴンのセットがあり、それらが互いに交差していないことを確認する必要があります（1つは別のポリゴンに完全に含まれている可能性があります。それで問題ありません）。これは、あるポリゴンと他のポリゴンの頂点ごとの内部性を確認するだけで確認できます。

また、包含ツリーを決定する必要があります。これは、どのポリゴンに特定のポリゴンが含まれるかを示す一連の関係です。ポリゴンは他のポリゴンと交差できないため、含まれているポリゴンには一意のコンテナがあります。「次に大きい」もの。つまり、AにBが含まれ、BにCが含まれている場合、AはBの親であり、BはCの親であり、AをCの親とは見なしません。

質問：封じ込め関係を効率的に決定し、交差しない基準を確認するにはどうすればよいですか？それぞれの問題を個別に解決するよりも、組み合わせたアルゴリズムの方が効率的かもしれないので、これを1つの質問として尋ねます。アルゴリズムは、頂点のリストによって指定されたポリゴンのリストを入力として受け取る必要があります。ブールBを生成して、どのポリゴンも他のポリゴンと交差していないかどうかを示します。また、B = trueの場合、ポリゴンPが子Cの親であるペア（P、C）のリストを生成します。

これは宿題ではありません。これは私が取り組んでいる趣味のプロジェクトのためのものです。

ほぼ球形である必要がある形状の表面を表す点のコレクションがあり、この形状内に他の特定の点があるかどうかを判断する方法が必要です。以前は形状を正確な球体として近似していましたが、これは不正確すぎることが判明したため、より正確な方法が必要です。完全な精度よりも単純さと速度が優先され、適切な近似値で十分です。

点群を 3D メッシュに変換する手法を見つけましたが、見つけたもののほとんどは非常に複雑で、できるだけ単純なものを探しています。

何か案は？

フライトシムのウェイポイントにランダムな場所を設定できる必要があります。数学の課題は簡単です。

「四角形内の単一のランダムな場所を見つけること。ポイントが任意の場所にある可能性が同じです。」

視覚的にこのように：

ABCD四角形の例は次のとおりです。A：[21417.78 37105.97] B：[38197.32 24009.74] C：[1364.19 2455.54] D：[1227.77 37378.81]

あなたが提供できるどんな助けにも前もって感謝します。:-)

編集お返事ありがとうございます。私は週末にこれを見て、その時に受け入れられた答えを授与します。ところで、四角形は凸面または凹面にすることができることを述べておかなければなりません。Sry'試合データ。

重複の可能性：
ブルートフォース検索とは別に、凸包で最大の三角形を見つける方法

私は頂点のそれぞれがそれらの点の1つにある領域ごとに最大の三角形を見つけたいランダムな点のセットを持っています。

これまでのところ、最大の三角形の頂点は点群 (または凸包) の外側の点にのみあることがわかったので、それを行う関数をプログラムしました (nlogn 時間でグラハム スキャンを使用)。

しかし、それは私が立ち往生しているところです。これらのポイントから最大の三角形を見つける方法を理解できる唯一の方法は、凸包アルゴリズムが通常大多数のポイントを追い出すため、平均的なケースではまだ許容できる n^3 時間でブルート フォースを使用することです。ただし、点が円上にある最悪のシナリオでは、この方法は惨めに失敗します。

これをより効率的に行うアルゴリズムを知っている人はいますか?

注：CGALにはこのアルゴリズムがあることは知っていますが、その方法については詳しく説明していません。私はライブラリを使用したくありません。これを学び、自分でプログラムしたいです (また、他の実装が共線点を拾うグラハムスキャンのように、操作したい方法に正確に微調整できるようにします)私はほしくない）。

2D平面内の2つの三角形間のオーバーラップ領域の面積を計算する必要があります。奇妙なことに、私は三角形の円の問題のコードを作成しました。これは非常にうまく機能しますが、三角形の三角形の問題に問題があります。

私はすでに、一方がもう一方を完全に含んでいるかどうか、またはもう一方が最初のものを含んでいるかどうかを確認し、すべてのエッジ方向の交点を取得します。これらの交点（ダビデの星のように最大6）は、他の三角形内に含まれる三角形の頂点と組み合わされて、交点領域の頂点になります。これらの点は凸多角形を形成する必要があります。

私が求める解決策は、次のいずれかの質問に対する答えです。

1. すべての人が知っている点のセットが点集合の凸包上にあるとすると、凸包の面積を計算します。それらはランダムな順序であることに注意してください。
2. 半平面のセットが与えられた場合、交差する領域を決定します。これは、両方の三角形を3つの半平面の交点として記述し、この記述の直接の交点として解を計算することと同じです。

質問1では、考えられるすべての三角形のすべての領域を単純に合計し、次にカウントの多重度で割ることを検討しましたが、それはばかげているようで、正しいかどうかはわかりません。トリックを行うある種のスイープラインアルゴリズムがあるように感じます。ただし、ソリューションは比較的数値的に堅牢でなければなりません。

質問2を解決する方法がわからないだけですが、一般的な答えは非常に役立ち、コードを提供することで1日を過ごすことができます。これにより、凸多角形で三角形分解を実行する代わりに、凸多角形の交差領域を直接計算できます。

編集：2つの凸多角形の交差多角形を見つけるための一般的なケースを説明するこの記事を知っています。三角形だけに関係しているように見えます。さらに、結果のポリゴン自体は実際には必要ありません。したがって、この質問は、この時点で怠惰に行われている可能性があります。