問題タブ [directed-acyclic-graphs]

プロパティのリストを表すDAGがあります。これらのプロパティは、a> bの場合、aがbに向けられたエッジを持つようなものです。これも推移的であるため、a>bおよびb>cの場合、aはcに向けられたエッジを持ちます。

ただし、aはbに向けられたエッジを持ち、bはcに向けられたエッジを持っているため、aからcへの向けられたエッジは不要です。これらの余分なエッジをすべて削除するにはどうすればよいですか？最小スパニングツリーアルゴリズムを使用することを考えていましたが、この状況で適用する適切なアルゴリズムが何であるかはよくわかりません。

各ノードとそのすべての出力エッジから深さ優先探索を実行し、特定のエッジを使用せずに特定のノードに到達できるかどうかを比較できると思いますが、これはひどく非効率的で遅いようです。

アルゴリズムが完了すると、出力はグラフと一致する順序ですべてのノードの線形リストになります。したがって、aにb、c、およびdへの3つの有向エッジがある場合。bとcもそれぞれdに向けられたエッジを持ち、出力はabcdまたはacbdのいずれかになります。

私の webapp には、他のフィールドを合計する多くのフィールドがあり、それらのフィールドはさらに多くのフィールドを合計します。これが有向非巡回グラフであることは知っています。

ページが読み込まれると、すべてのフィールドの値が計算されます。私が実際にやろうとしているのは、フィールドを計算するための効率的な順序を含む 1 次元のリストに DAG を変換することです。

例: A = B + D、D = B + C、B = C + E 効率的な計算順序: E -> C -> B -> D -> A

現在、私のアルゴリズムは List への単純な挿入を繰り返し行うだけですが、それが壊れ始める状況に遭遇しました。代わりに、すべての依存関係をツリー構造に変換し、そこからそれを 1 次元形式に変換する必要があると考えています。このようなツリーを効率的な順序付けに変換するための簡単なアルゴリズムはありますか?

私はDAGを持っています。この操作で、2 つのノード間にエッジを追加します。

A が B から到達可能な場合、B は A の親です。A が別のノードを経由せずに B から到達できる場合、B は A の直接の親です。

このグラフの要件は次のとおりです。

1. サイクルなし。
2. どのノードにも、直接の親のリスト P[1]、P[2]、P[3] があります... P[i] は、任意の i と j の P[j] の親ではありません。

エッジを追加する場合、要件 1 が満たされない場合、エッジは構築されません。エッジを追加する場合、要件 2 が満たされない場合、エッジが構築されますが、要件 2 が満たされるように直接の親が変更されます。

たとえば、3 つのノードがあります。

• A、直系の父母：なし
• B、直系の親：A
• C、直系の親：A

ここで、B と C の間にエッジを追加すると、次のようになります。

• C、直接の親: A、B

しかし、A は B の親であり、要件 2 を満たしていないため、A は C の直接の親から削除され、次のようになります。

• C、直系の親：B

現在、私がやったことは次のとおりです。AからBにエッジを追加します（このAはBの親になります）

1. B が A の親であるかどうかを BFS で確認します。その場合は、エッジを追加しないでください (これにより、サイクルがないことが確認されます)。
2. A がすでに B の親であるかどうかを BFS で確認します。その場合は、エッジを追加しないでください。
3. A の親と B の直接の親との交点を見つけます。これは、BFS を介して A のすべての親を見つけることによって行われます。B の直接の親から交差を削除し、A を B の直接の親として追加します (2 と 3 で要件 2 を満たしていることを確認します)。

これは遅いです。5kノードレベルで故障し（100kノード未満のグラフを処理するためにこれを探しています）、速度が許容できなくなり、ノードエッジを追加するのに0.02秒かかります。

ステップ1と2は、他のアルゴリズムを使用して1ステップで実行できると感じています。

トポロジー順序付けを使用することを考えましたが、グラフ全体を横断する必要があり、これはステップ 1 と 2 の最悪のケースです。新しいノードが追加されると、順序が乱れます。そのため、挿入のたびにトポロジー順序付けを実行する必要があるため、メリットはありません。ステップ 3 では、A の親のセット全体を見つける必要があります。平均してグラフのかなりの部分を横断するため、プロセスはかなり遅くなります。

これをより効率的にするにはどうすればよいですか？

sとtの頂点を持つグラフがあり、その間の最短経路を見つける必要があります。グラフには、私が利用したい多くの特別なプロパティがあります。

• グラフはDAG（有向非巡回グラフ）です。
• 従来のO（| V + E |）よりも速く、O（| V |）時間でトポロジカルソートを作成できます。
• トポロジカルソート内で、sはリストの最初の項目であり、tは最後の項目です。

トポロジカルソートの頂点を取得すると、ダイクストラの均一コストの現在の標準よりも速く最短経路を見つけることができると言われましたが、そのアルゴリズムを見つけることができないようです。

擬似コードをいただければ幸いです。

編集：sからtまでのすべてのパスは同じ数のエッジを持っています。エッジには重みがあります。最低コストのパスを探しています。

各ノードがカテゴリに属する​​ DAG が与えられた場合、このグラフを各カテゴリの列を持つテーブルに変換するにはどうすればよいでしょうか? 変換は可逆的である必要はありませんが、グラフの構造に関する有用な情報を保持する必要があります。グラフとテーブルを見ている人がどの行にも驚かされないという意味で、「自然な」変換である必要があります。また、コンパクトにする必要があります。つまり、行がほとんどありません。

たとえば、エッジ a1->b1、a1->b2、b1->c1、b2->c1 を持つノード a1、b1、b2、c1 のグラフ (つまり、ひし形のグラフ) が与えられた場合、次のようになると予想されます。テーブル：

私はこの問題についてかなり考えましたが、特定のグラフで直感的な結果が得られるアルゴリズムを思いつくのに苦労しています。エッジ a1->c1、b1->c1 を持つグラフ a1、b1、c1 を考えてみましょう。アルゴリズムでこのテーブルを生成したいと思います:

しかし、代わりにこれを生成する必要があります。

問題に対する創造的なアイデアと洞察を探しています。役立つと思われる場合は、問題を単純化または制限するために自由に変更してください。

ブレインストーミングしましょう！

編集：

行の順序は関係ありませんが、変換では常に同じ行セットが生成されます。

テーブルは、Excel などを使用して並べ替えやフィルタリングを行うときに適切に動作するはずです。つまり、複数のノードをテーブルの 1 つのセルにパックすることはできません。セルごとに 1 つのノードのみです。

先日、私は自分自身を正しく表現できず、答えを閉じてしまったので、ここに私の2番目のショットがあります:

基本的な DAG (有向非巡回グラフ) アプリケーションを作成する必要があり、ノード ベースのアプリケーションという一般的な用語を使用します。ツリー全体を実行するコンソールの例だけで、nw の GUI は必要ありません。

これが私がこれまでに持っているものです:

ノードは、任意の数の入力と任意の数の出力を持つことができます (どのように処理すればよいですか?)

私の質問は次のとおりです。ノード合計の出力がノード ルートの入力であり、その出力がノード Output_screen の入力である DAG を構築するにはどうすればよいですか?

ノード(合計)---> ノード(ルート)--->ノード(出力画面)

私はそれについて何も見つけることができなかったので、私はどんな助けにも感謝します

ここにツリーがあります：

1. ルートは1つになります。

2. 各ツリー ノードには、0 個以上の子があります。

3. 2 つのノードが同じ子を指すことができます。ノード A とノード B の両方に子 C があるとします。

ただし、禁止事項として、

ノード A はノード B の子孫であり、ノード B はノード A の子孫です。

禁止されているケースの 1 つは、

ノード A には子ノード C とノード D があり、

ノード C と D の両方に子ノード E があり、

ノード E には A の子があります。

問題は、この円を最速で決定する方法です。

更新:これは、有向グラフで任意のサイクルを見つけることだと認識しています。たった今、Tarjan のアルゴリズムに似た解決策を考え出すことができました。

コメントありがとうございます。

有向非巡回グラフとは何かを簡単に説明してもらえますか？私はウィキペディアを見てきましたが、プログラミングでの使用を実際に見ることはできません。

次の問題を解決するために、適度なスペース要件で高速なアルゴリズムを見つけようとしています。

DAG の各頂点について、DAG の推移閉包の入次数と出次数の合計を求めます。

この DAG を考えると:

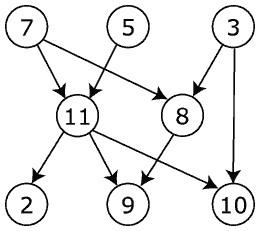
次の結果が期待されます。

これは、推移閉包を実際に構築しなくても可能であるように思われます。この問題を正確に説明するものをネット上で見つけることができませんでした。これを行う方法についていくつかのアイデアがありますが、SO クラウドが何を思いつくかを見たかったのです。