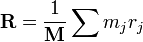3

私は C# 2d ソフト ボディ物理エンジンに取り組んでおり、指定されたオブジェクトの頂点に質量を割り当てる必要があります: 頂点のリスト (x、y 位置)、オブジェクトの総質量、および質量の中心。

重心は次のように与えられます。

代替テキスト

どこ、

R = center of mass
M = total mass
mj = mass of vertex j
rj = position of vertex j

R、M、および rj を指定して、各 mj を概算できるアルゴリズムが必要です。

編集:無限の解決策があることを認識していることを明確にしたいだけです。mj のセットを見つける簡単なアルゴリズムを探しています (それらがそれぞれ mj = M/[頂点の数] に十分近く、「十分に」が小さな浮動小数点のしきい値として定義されている)。

また、各オブジェクトは約 5 ～ 35 ポイントで構成されます。

4

4 に答える 4

2

均一な密度のポリゴンの CM は、次のように計算できます。N 個の頂点に 0..N-1 の番号を付け、それらを循環的に処理して、頂点 N が頂点 0 にラップするようにします。

total_area = sum[i=0..N-1]( X(p[i],p[i+1])/2 )
CM = sum[i=0..N-1]( (p[i]+p[i+1])*X(p[i],p[i+1])/6 ) / total_area

   where X(p,q)= p.x*q.y - q.x*p.y  [basically, a 2D cross product]

多角形が凸状の場合、CM は多角形の内側にあるため、CM をハブとして領域をパイのように三角形にスライスすることから合理的に開始できます。CM を変更せずに、三角形の各頂点にその質量の 3 分の 1 の重みを付けることができるはずですが、それでも、ポリゴン全体の CM に総質量の 3 分の 1 が残ることになります。それにもかかわらず、物質移動を 3/2 でスケーリングすると、各三角形の質量を 2 つの「外部」頂点間で分割できるはずです。結果として、

area[i] = X( (p[i]-CM), (p[i+1]-CM) ) / 2
   (this is the area of the triangle between the CM and vertices i and i+1)

mass[i] = (total_mass/total_area) * (area[i-1] + area[i])/2

この種の物質移動は非常に「非物理的」であることに注意してください。文字通りに扱われれば、慣性モーメントをひどく台無しにしてしまうでしょう。ただし、頂点間で質量を分散する必要があり (ある種の安っぽい爆発の場合など)、その際に CM を混乱させたくない場合は、これでうまくいくはずです。

最後に、いくつかの警告:

  • これは実際のCMを使わないとうまくいきません
  • これを凹状のオブジェクトに使用するのは危険です。負の質量になるリスクがあります
于 2010-01-25T10:08:49.857 に答える
1

重心 R は、頂点が移動するにつれて常に変化します。したがって、10 個の頂点がある場合は、10 個の連続した「フレーム」からの値を保存します。これにより、10 個の未知数に対して 10 個の方程式が得られます (質量が時間の経過とともに変化しないと仮定します)。

于 2010-01-25T01:47:26.110 に答える
1

自由度を数えます:D次元空間の点については、D+1方程式[+] と個別の粒子nの未知数があります。nあなたn>D+1が沈んだ場合（あなたが私たちに言ったよりも多くの情報を持っていない限り：対称制約、高次モーメントなど...）。

編集:私の以前のバージョンでは、s があり、m_is を探していると想定していましたr_i。r_is があり、 sが必要な場合は、わずかに優れていますm_i。

[+]上にリストしたもの（実際のD別の方程式）とM = \sum m_j

アリウ氏は次のように述べています。

申し訳ありませんが、私はあなたの質問を誤解しました。トーラス、ドーナツ、リングなどのオブジェクト (カットアウトのあるオブジェクト...) をモデリングしているかどうかを尋ねていると思いました。外側のシェル (風船や泡など) だけでボディをモデリングしています。それ以上に複雑なことは必要ありません。

今、私たちはどこかに到達しています。あなたはもっと何かを知っています。

オブジェクトを隣接点間の三角形に分割することで、オブジェクトの表面積を概算できます。この総面積から平均質量密度が得られます。次に、自由度の不足を見つけ、その多くr_iの s (ランダムに描かれたと思います) に、平均密度とそれが関係している各三角形の面積の 1/3 に基づいて初期質量を割り当てます。次に、残りのシステムを解析的に解きます。問題の条件が悪い場合は、割り当てられた点の新しいセットを描画するか、既に推測した質量でランダム ウォークを試みることができます。

于 2010-01-24T20:31:58.737 に答える
0

私は問題をひっくり返します。つまり、オブジェクトの密度と位置（もちろん、オブジェクトの重心と、オブジェクトの方向に対応する3つのベクトル、オイラーの角度を参照）が与えられると、各頂点でボリュームがそれに関連付けられます。要素（解像度によって変化し、オブジェクトのエッジの位置では分数になる可能性があります）、密度（d_j）に関連するボリューム（v_j）を掛けます。m_j= v_j*d_j。このアプローチは、オブジェクトの重心を自然に再現する必要があります。

おそらく私はあなたの問題を理解していませんでしたが、これは最終的に正しい質量（Mass = sum（m_j）= sum（v_j * d_j））をもたらし、最悪の場合、このアプローチはあなたの結果の検証をもたらすと考えます。

于 2010-01-25T01:26:47.493 に答える