10

タッチ スクリーン UI のスクロール動作を実装していますが、今は疲れすぎて、おそらく些細な数学に頭を悩ませることができません。

y (distance/velocity)
|********
|        ******
|              ****
|                  ***
|                     ***
|                        **
|                          **
|                            *
|                             *
-------------------------------- x (time)

f(x)→?

UI は、ユーザーがビューを任意の方向にドラッグして「投げる」ことができ、画面から指を離した後もしばらくスクロールし続けることができるようになっています。ユーザーが指を離す前にどれだけ速くドラッグしていたかに依存する、一種の勢いがあります。

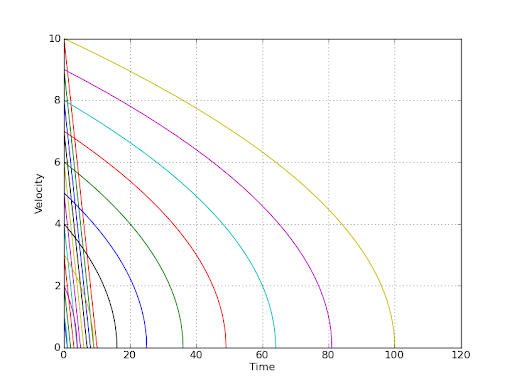
したがって、開始速度 (v0) があり、20 ミリ秒ごとに現在の速度に相対的な量だけスクロールします。スクロールを繰り返すたびに、速度がしきい値を下回るまで速度を少し下げて停止します。固定量 (線形) だけ減分すると正しく見えないので、負の加速度をモデル化する必要がありますが、速度を下げる必要がある量を計算するためのまともな単純な式を思い付くことができません。すべての反復で。

アップデート：

これまでの回答に感謝しますが、まだフィードバックから満足のいく機能を引き出すことができませんでした. 希望するソリューションを十分に説明できていない可能性があるため、どのような計算を行いたいかを示す実際の例を示します。

ある通りをある車が走っていて、運転手が車が止まるまで最大までブレーキを踏んだとします。運転手は、同じ道路で同じ車でこれを複数回行いますが、さまざまな速度でブレーキをかけ始めます。車が減速している間、現在の速度のみに基づいて、正確に 1 秒後の速度を計算できるようにしたいと考えています。この計算では、すべての環境要因が同じままであるため、ドライバーがブレーキを踏み始めたときに車が運転していた速度は関係ありません。もちろん、数式にはいくつかの定数がありますが、車が 30 m/s まで下がった場合、ドライバーがブレーキをかけ始めたときに 100 m/s で運転していたか 50 m/s で運転していたかに関係なく、次の 1 秒間に同じ距離を進みます。 . そのため、休憩を打ってからの時間も関数のパラメーターにはなりません。特定の速度での減速度は常に同じです。

このような状況で、減速度、質量、摩擦などの任意の定数を仮定し、空気抵抗などの複雑な影響を無視して、1 秒後の速度をどのように計算しますか? 私が求めているのは、運動エネルギーと、車の破損による摩擦による散逸です。

更新 2 車の加速が線形であることがわかりましたが、これは実際には私が探していたものではありません。これを片付けて、明日新しい提案を試してみます。これまでにご意見をお寄せいただきありがとうございます。

4

15 に答える 15

8

[短い回答（C構文を想定）]

double v(double old_v, double dt) {
    t = t_for(old_v); 
    new_t = t - dt; 
    return (new_t <= 0)?0:v_for(t);
}

double t_for(double v)およびdouble v_for(double t)は、v から t への双方向マッピング (数学的な意味での関数) からの戻り値です。これは、単調であり、 に対して定義されているという制約を伴う任意ですv >=0(したがって、 の点がありますv=0)。例は次のとおりです。

double v_for(double t) { return pow(t, k); }
double t_for(double v) { return pow(v, 1.0/k); }

どこに：

  1. k>1時間の経過とともにモジュロで減少する減速度を与えます。
  2. k<1時間の経過とともにモジュロで増加する減速を与えます。
  3. k=1一定の減速を与えます。

[より長いもの (理論的根拠とプロット付き)]

したがって、本質的な目標は次のとおりです。

  1. v(t+dt)=f(v(t),dt)現在の速度値vと時間デルタを取りdt、その瞬間の速度を返す関数を見つけること(既に既知であり、パラメータとして提供され、単なる時間デルタであるためt+dt、実際に指定する必要はありません)。つまり、タスクは、特定のプロパティを持つルーチンを実装することです (以下を参照)。tv(t)dtdouble next_v(curr_v, dt);

  2. [注意してください] 問題の関数には、以前のベロシティ変更の「履歴」に関係なく、同じ結果を返すという便利な(そして望ましい)プロパティがあります。つまり、たとえば、一連の連続する速度が [100, 50, 10, 0] (開始時の速度v0=100) である場合、これよりも大きい他のシーケンスには同じ「テール」があります: [150, 100, 50, 10, 0] (開始速度v0=150) など。つまり、開始速度に関係なく、すべての速度から時間へのプロットは、時間軸に沿ってそれぞれ独自の値だけオフセットされた互いのコピーになります。 (下のグラフを参照してください。線t=0.0と線の間のプロットの部分t=2.0が同一であることに注意してください)。

  3. さらに、加速度w(t)=dv(t)/dtは時間の降順関数でなければなりませんt(ここでモデル化する移動 GUI オブジェクトの視覚的に快適で「直感的な」動作のため)。

提案されたアイデアは次のとおりです。

  1. 最初に、目的のプロパティを持つ単調速度関数を選択します (この場合、加速度は徐々に減少しますが、以下の例に示すように、「加速された」関数を使用する方が簡単です)。この関数には上限も設定しないでください。これにより、どんな大きな速度値にも使用できます。また、速度がゼロになるポイントが必要です。いくつかの例は次のv(t) = k*tとおりkです。v=sqrt(-t)t <= 0

  2. 次に、任意の速度について、上記の関数のプロットでこの速度値を持つポイントを見つけます (関数がバインドされていないためポイントがあり、単調であるためポイントは 1 つだけです)、より小さな速度に向かって時間デルタだけ進みます。次の値を取得します。反復により、徐々に (そして必然的に) 速度がゼロになるポイントに到達します。

  3. 基本的にこれですべてです。「最終」式を作成する必要さえなく、時間値または初期 (現在ではない) 速度への依存がなくなり、プログラミングが非常に簡単になります。

2 つの単純なケースでは、この小さな python スクリプトは以下のプロットを生成します (指定された初期速度は1.0から10.0です)。おわかりのように、任意の速度「レベル」と「下向き」から、プロットは同じように「動作」します。どの速度で減速（減速）し始めても、速度がゼロ（になる）ポイントまで同じ曲線に沿って「移動」しています。

import numpy
import pylab

import math


class VelocityCurve(object):
    """
    An interface for the velocity 'curve'.
    Must represent a _monotonically_ _growing_
        (i.e. with one-to-one correspondence
        between argument and value) function
        (think of a deceleration reverse-played)
    Must be defined for all larger-than-zero 'v' and 't'
    """
    def v(self, t):
        raise NotImplementedError

    def t(self, v):
        raise NotImplementedError



class VelocityValues(object):

    def __init__(self, v0, velocity_curve):
        assert v0 >= 0
        assert velocity_curve

        self._v = v0
        self._vc = velocity_curve

    def next_v(self, dt):
        t = self._vc.t(self._v)
        new_t = t - dt

        if new_t <= 0:
            self._v = 0
        else:
            self._v = self._vc.v(new_t)

        return self._v


class LinearVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=k*t'"""
        super(LinearVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return self._k*t

    def t(self, v):
        assert v >= 0
        return v/self._k


class RootVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=t^(1/k)'"""
        super(RootVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return math.pow(t, 1.0/self._k)

    def t(self, v):
        assert v >= 0
        return math.pow(v, self._k)


def plot_v_arr(v0, velocity_curve, dt):
    vel = VelocityValues(v0, velocity_curve)
    v_list = [v0]

    while True:
        v = vel.next_v(dt)
        v_list.append(v)

        if v <= 0:
            break

    v_arr = numpy.array(list(v_list))
    t_arr = numpy.array(xrange(len(v_list)))*dt

    pylab.plot(t_arr, v_arr)


dt = 0.1

for v0 in range(1, 11):
    plot_v_arr(v0, LinearVelocityCurve(1), dt)

for v0 in range(1, 11):
    plot_v_arr(v0, RootVelocityCurve(2), dt)


pylab.xlabel('Time ')
pylab.ylabel('Velocity')

pylab.grid(True)

pylab.show()

これにより、次のプロットが得られます (線形減速 (つまり、一定の減速) の線形プロット、「曲線」 - 「平方根」プロットの場合 (上記のコードを参照))。

また、上記のスクリプトを実行するには、 pylab、numpy 、およびその仲間がインストールされている必要があることに注意してください（ただし、プロット部分のみ、「コア」クラスは何にも依存せず、もちろん単独で使用できます）。

PSこのアプローチを使用すると、実際に「構築」できます（たとえば、さまざまなt間隔でさまざまな機能を拡張したり、手描きの（記録された）「人間工学的」曲線を滑らかにすることさえできます）彼が好きな「ドラッグ」:)

于 2010-02-20T02:47:24.663 に答える
5

コメントを読んだ後、答えを変更したいと思います。速度を指数関数的に減衰させるには、k = 0.955 のように、速度に k < 1 を掛けます。

説明（グラフと調整可能な方程式付き！）が続きます...

元の質問のグラフは、速度が開始値に近く、その後急速に減少していることを示していると解釈します。しかし、本をテーブルの上で滑らせることを想像すると、本はすぐにあなたから遠ざかり、減速し、惰性で停止します。@Chris Farmer使用する適切なモデルは、速度に比例する抗力であることに同意します。このモデルを使用して、上で提案した答えを導き出します。この長さについて事前にお詫び申し上げます。数学が得意な人なら、これをかなり単純化できると確信しています。 また、グラフへのリンクを直接入れました。リンクには、SO パーサーが気に入らない文字がいくつかあります。 URL は現在修正されています。

以下の定義を使用します。

x -> time
a(x) -> acceleration as a function of time
v(x) -> velocity as a function of time
y(x) -> position as a function of time
u -> constant coefficient of drag
colon : denotes proportionality

抗力による力は速度に比例することがわかっています。また、力は加速度に比例することもわかっています。

a(x) : -u v(x)        (Eqn. 1)

マイナス記号は、加速度が現在の移動方向と反対であることを保証します。

速度は積分加速度であることはわかっています。

v(x) : integral( -u v(x) dx )        (Eqn. 2)

これは、速度がそれ自体の積分に比例することを意味します。e^xがこの条件を満たしていることがわかっています。だから私たちはそれを仮定します

v(x) : e^(-u x)        (Eqn. 3)

指数の抗力係数は、式の積分を解くと次のようになります。2式に戻るためのuキャンセル。3.

次に、 の値を計算する必要がありますu。@BlueRaja指摘したように、x に関係なく、決してe^xゼロにはなりません。しかし、十分に負の x ではゼロに近づきます。元の速度の 1% を「停止」(しきい値の考え方) と考えて、 x = 2 秒以内に停止したいとしましょう (これは後で調整できます)。次に、解決する必要があります

e^(-2u) = 0.01        (Eqn. 4)

これにより、計算することができます

u = -ln(0.01)/2 ~= 2.3        (Eqn. 5)

グラフにしましょうv(x)。

指数関数的に 2 秒で小さい値に減衰するように見えます。ここまでは順調ですね。

GUI で必ずしも指数を計算する必要はありません。指数の底を簡単に変換できることはわかっていますが、

e^(-u x) = (e^-u)^x        (Eqn. 6)

また、時間を秒単位で追跡したくもありません。更新レートが 20 ミリ秒であることはわかっているのでn、ティック レートが 50 ティック/秒の timetick を定義しましょう。

n = 50 x        (Eqn. 7)

式から u の値を代入します。5を式に 6、式と組み合わせます。7、および式に代入します。3、私たちは得る

v(n) : k^n, k = e^(ln(0.01)/2/50) ~= 0.955        (Eqn. 8)

これを、新しい x 軸を timeticks でプロットしてみましょう。

繰り返しますが、速度関数は、必要な反復回数で 1% に減衰する何かに比例し、「摩擦の影響下で惰性走行」モデルに従います。これで、初速度v0に式を掛けることができます。8 任意のタイムステップ n での実際の速度を取得するには:

v(n) = v0 k^n        (Eqn. 9)

実装では、v0! を追跡する必要がないことに注意してください。v0 * k^n閉じた形式を再帰に変換して、最終的な答えを得ることができます

v(n+1) = v(n)*k        (Eqn. 10)

この答えは、初期速度が何であるかを気にしないという制約を満たします。次の速度は常に現在の速度だけを使用して計算できます。

位置の動作が理にかなっていることを確認することは価値があります。このような速度モデルに従う位置は

y(n) = y0 + sum(0..n)(v(n))        (Eqn. 11)

式の合計。11 は、式 9 の形式を使用して簡単に解決できます。インデックス変数 p の使用:

sum(p = 0..n-1)(v0 k^p) = v0 (1-k^n)/(1-k)        (Eqn. 12)

だから私たちは持っています

y(n) = y0 + v0 (1-k^n)/(1-k)        (Eqn. 13)

y0 = 0これをと でプロットしましょうv0 = 1。

そのため、原点から急速に離れ、優雅な海岸線をたどって停止することがわかります。このグラフは、元のグラフよりもスライドをより忠実に描写していると思います。

k一般に、式を使用して調整できます。

k = e^(ln(Threshold)/Time/Tickrate)        (Eqn. 14)
where:
Threshold is the fraction of starting velocity at which static friction kicks in
Time is the time in seconds at which the speed should drop to Threshold
Tickrate is your discrete sampling interval

( @pokeWolfram Alpha をプロットに使用する方法をデモンストレーションしてくれてありがとう - とてもすばらしいです。)

古い答え

k = 0.98 のように、速度に k < 1 を掛けて、指数関数的に減衰させます。

于 2010-02-19T18:56:16.480 に答える
4

車が減速している間、現在の速度のみに基づいて、正確に 1 秒後の速度を計算できるようにしたいと考えています。

それが加速度の定義です。たとえば、加速度がa = -9 meters/sec/secで、20 meters/sec現在の速度が である場合、1 秒後の速度は になります11 meters/sec。

Δv言い換えると、現在と数秒後の速度の変化t(一定の加速度を仮定) は次のようになります。

Δv = a*t

での初期速度(この速度は v 0と呼ばれる) が与えられると、いつでも速度の (古典物理学) 方程式はtt=0

v(t) = v0+ a*t

微積分クラスの最初の 2 週間で学習することを使用して、上記の式からx(t)(時間における車の距離) の式を取得することもできます。tこれはあなたに与えるでしょう

x(t) = x0 + v0 *t + 0.5*a*t2

(微積分なしでこれを導出することも可能です。こちらを参照してください)

最後に、これを物理シミュレーションではなくゲームで行う場合 (つまり、正確な結果は必要ありません)、フレームごとに位置を再計算するのではなく、フレームごとに位置と速度を単純に変更することをお勧めします。これを行うには、速度 (および加速度) がピクセル/秒 (-per-second) で測定されると仮定して、フレームごとに次のことを行う必要があります。

velocity_new = velocity_old + acceleration/frames_per_second
position_new = position_old + velocity_old/frames_per_second
于 2010-02-20T01:54:17.517 に答える
2

時間の経過とともに増加する減速を探しているようです。

計算してみてください

Delta_v = -(A*t + B)、適切な定数AおよびBを選択します。

tはその時点までの合計時間です。

を追加して速度を変更しますDelta_v。

これは基本的に線形の負の加速度に対応します。

基本的に、時間の経過とともに増加する関数を選択できます（たとえばf（t））

と計算

Delta_v = -f(t)

f（t）を適切に選択すると、希望する効果が得られます。

使用できるいくつかの例：

f(t) = At + B.
f(t) = A*exp(Bt)

もちろん、少し遊んで、正しい定数を見つけようとする必要があります。

于 2010-02-19T19:29:58.890 に答える
2

感想も添えておきます。一定の（負の）加速が必要ないようです。その結果、次のような方程式が得られます。

v(t) = v(0) + a*t,

ここaで、 は負の加速度、tは時間、 は時間v(t)における速度tです。これにより、以下が得られます。

v(t2) - v(t1) = a(t2-t1),

これは、与えられた Δt に対して、速度差が aΔt (定数) に等しいことを意味します。

あなたが探しているのは、現在の速度に依存する「摩擦」項です。その仮定の下では、速度の変化率は現在の速度に比例します。

d v(t) / d t = -b*v(t).

上記を解くのは簡単で、v(t) = v(0) e −btが得られます。

この式を積分すると、x(t) = v(0)(1−e −bt ) / b が得られます。ここで、x は位置です。v(0) = 1、b = 0.1の位置プロット1は、使用できるもののように見えます。b の値をいじって、等式にスケール係数を追加することは、あなたがやりたいことかもしれません。

1 http://www.wolframalpha.com/input/?i=plot+%281+-+1+e^%28-0.1+x%29+%29+%2F+0.1+for+x+%3D+0+to+100

于 2010-02-20T03:36:25.780 に答える
2

反復ごとに一定量だけ速度を下げることができます。例: 50 の速度で開始し、次の反復で 40、次に 30、20、10 で停止します。これは、速度に関係なく、一定の「摩擦」を表し、これは実際にはかなり現実に近いものです (ウィキペディアの摩擦を参照してください)。

この外観が気に入らない場合は、摩擦を速度に依存させる必要があります。係数がかなり小さい線形関係friction = base-friction + (coefficient * velocity)で十分だと思います。

于 2010-02-19T21:16:54.857 に答える
2

mtrw's answer のコメントで述べているように減速を増やしたい場合で、物理的なリアリズムについてあまりうるさくない場合は、以下の式が探しているものになる可能性があります。

V(t+dt) = V(t) - K1 + K2 x V(t)

V(t)= 現在の速度 V(t+dt)= 次回のインクリメントでの速度 K1 と K2 は、校正する定数です。(K2 x Vmax) < K1 であることを確認してください。そうしないと、高速で加速します。

それでもうまくいかない場合は、V(t+dt) = V(t) - K1 + K2 xf(V(t)) を試してください。

ここで、f(x) は選択した単調増加関数で、フィーリングをどこに取りたいかによって、平方根または平方根になる場合があります。可能なすべての V(t) に対して (K2 xf(V(t))) < K1 であることを確認してください。

(単調増加関数は、x が増加すると f(x) が常に増加することを意味します)

于 2010-02-20T02:47:47.813 に答える
1

速度の非線形変化は、加速度が一定でないことを意味します。一定でない加速度は、システムがジャークの影響下にあることを意味します。すべての加速度方程式を取り、「(1/6)jt 3」を追加します。a を固定し、v が 0 になるまで ja に小さな負の値を与えます。

于 2010-02-20T02:57:36.720 に答える
0 
y(x) = y0 - a * e ^ ( k * x )

ここy0で、は開始定数、aおよびkは係数です。

プロットの例。

于 2010-02-20T17:56:25.717 に答える
0

v=v*0.9 のように速度を下げると、停止した速度と見なされる速度になります。このようにして、オブジェクトは最終的に静止し、移動中にリソースを消費し続けることはありません。for(v=startingVelocity;v<1.0;v*=0.9) { x+=v; のようなものです。}

于 2010-02-19T19:38:29.087 に答える
0

車の例についての、プログラミング以外のちょっとした議論。

まず、運転手は高速でブレーキをロックできないと仮定します。

ほとんどの新しいドライバーが最初に (あるいは 2 番目または 3 番目に) 学ぶことは、ブレーキをかけるときの自然な傾向は、ブレーキ ペダルを固定位置に保持することであるということです。その結果、車がゆっくりと動いていたところから停止するようになると、突然前に飛び出します。これは、ブレーキが、制動力がブレーキ圧力に比例する動摩擦から、制動力が車の前進運動量を復元する静摩擦に移行するために発生します。この急激な加速は不快であり、新しいドライバーは減速の最後にペダルを踏んで停止することを学びます。

この挙動は別の特異性を覆い隠していますが、これはマニュアル トランスミッション車での通常の加速中に気付くことができます。加速中 (または減速中) に、ドライバーが突然トランスミッションのギアを外すと、すべての乗客が突然前に飛び出します。実際に起こっていることは、彼らを座席の後ろに押し付けていた加速力が突然取り除かれ、ニュートラルな座位に跳ね返ることです。より快適な運転方法は、エンジンの動力が徐々に取り除かれるように、クラッチを徐々にフェザーすることです。

どちらの場合も、より美しいドライビング スタイルには、加速を滑らかにし、突然のジャンプを取り除くことが含まれます。これは基本的に、連続二次導関数について話す別の方法です。このプロパティを使用すると、ほとんどすべての動きが自然に見えます。

于 2010-02-20T04:40:30.987 に答える
0

私はこれを試しましたが、これは(Rubyで)動作します。計算が正しいかどうかはわかりませんが、出力は正しいように見えます。つまり、中心に近づくにつれて速くなります。

velocity=100;
(100.downto(0)).each { |distance_from_black_hole |  velocity=velocity+9.8/distance_from_black_hole; puts velocity; }
于 2010-02-20T03:11:38.293 に答える
0

速度を追跡し、毎回速度の何分の一かを減らすことができます。それは摩擦を非常によくシミュレートすると思います。

于 2010-02-19T18:56:44.483 に答える
0

加速度は、速度の 1 次微分と距離の 2 次微分です。あなたのグラフは、いくつかの定数 C と k に対して Ck*x^2 のような二次放物線のように見えます。y が実際に距離である場合は a=-2k が必要であり、y が速度である場合は a=-2kx が必要です。いずれの場合も、速度 v(x) = V0 + a(x)*x です。(ここで、x は実際の時間です。私はあなたの慣例に従い、t を使用していません。)

于 2010-02-19T19:55:19.723 に答える
0 
加速度 = (力 / 質量)
速度 = (加速度 * 時間)
(ユーザーの指からの力) = 加速度 / 質量 = 速度 / 時間
  1. ビューに質量を与えます（物事が合理的に見えるまで微調整し、ユーザーに微調整させます）
  2. いくつかの新しい力を特定する (ドラッグ)
  3. 新しい力 (ドラッグ) にマグニチュードを与える (妥当になるまで微調整し、ユーザーに微調整させます)
  4. オブジェクトに新しい力を適用し、速度が低下するのを確認します
于 2010-02-19T18:59:30.630 に答える