1

この質問に触発されて、質問者は、システムのユーザーが互いにまったく同時に何らかのアクションを実行することはめったにないと想定しています。

そのような仮定をすることについて私が知っていることを考えると、ユーザーが実際に同時に物事を行うことを保証できます。しかし、予想される衝突の頻度を実際にどのように計算するかについて、私は途方に暮れています。

たとえば、各ユーザーが3分ごとにアクションを実行していて、タイマーが実際にはミリ秒までしか正確でないと仮定した場合、衝突の頻度を計算するための式は何ですか？

ウィキペディアの誕生日の問題のエントリは、次の式に一般化できます。 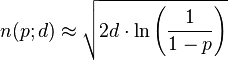誕生日の問題 ここで、dは180,000ミリ秒、pは衝突の確率です。

したがって、3人のユーザーが言うと、衝突が発生する3分間の確率は2.4996E-05になります。

問題は、日中の衝突の可能性はどのくらいになるのでしょうか。稼働日には60-*60 * 8/3 = 9600 3分の期間があるため、特定の日の衝突の確率は1-（（1-2.4996E-05）^ 9600）= 21％になります。物事が洋ナシの形になる可能性はかなり高いです。

4

5 に答える 5

2

3分で180000ミリ秒になります。ユーザーの数がわかっている場合は、誕生日のパラドックスの確率を使用して、衝突の確率を判断できます。

タイマーはミリ秒単位で測定される場合でも、ミリ秒単位で正確でない可能性があることも考慮してください。多くのタイマーは、1秒間に1000回未満実行されるティックに基づいています。

于 2011-02-23T03:29:16.733 に答える
1

3分=180秒=180000。このMをミリ秒単位で呼び出します。

何人のユーザーがいますか？Nがあるとしましょう。

3分間で、ユーザー1は1ミリ秒（180000は無料、180000は可能）を飲み込みます。これは、180000/180000=1回の成功のチャンスです。

次の男：179999/180000のチャンスで良いスロットを手に入れましょう。次の男：179998/180000良いスロットを獲得するチャンス。

それらすべての可能性は

 180000 * 179999 * 179998 . . .
--------------------------------
 180000 * 180000 * 180000 . . .

要するに：

 N! / ((N^N)*(N-M)!)
于 2011-02-23T03:23:36.913 に答える
1

衝突の頻度を取得するには、1 mS間隔での衝突の確率を取得してから、任意の間隔にスケールアップします（たとえば、1000を掛けて、1秒あたりの衝突を取得します）。

その確率を取得するには、1 mSの時間間隔で衝突が発生しない確率を取得しますか？これは、その間隔中に行動するユーザーの数が1または0である確率です。

ユーザーがいてn、特定のユーザーが時間間隔中に行動する確率がである場合p、

P（0）=（1-p）n = 1-np + n（n-1）p 2/2 -...
P（1）= np（1-p）n-1 = np-n（n -1）p 2 + ...
P（0または1）= 1-n（n-1）p 2/2 + ...
P（1より大きい）= n（n-1）p 2/2 + ..。。

ここで、いくつかの数値をプラグインします。3分ごとに1回、p = 1.8x10 -5になるため、衝突の確率はおよそ

n（n-1）（3.24x10 -10）

したがって、私の計算が正しければ、100人のユーザーがいる場合、10分ごとにおよそ1回の衝突が発生します。

于 2011-02-23T04:05:46.423 に答える
0

この質問の重要な点は、ある間隔でイベントが発生する確率を知り、イベントが完了するまでにかかる時間を知ることです。次に、両方の確率は、最初のイベントの確率を条件として、最初のイベントの期間中に発生する2番目のイベントの確率になります。

これで、一般にベイズの定理に基づいてこれを計算できます。

于 2011-02-23T03:20:39.660 に答える
0

CollisionFreqPercent =（AccuracySecs /（ActionDelaySecs / ConcurrentUsers））* 100;

例えば：

1ユーザー=（0.001 /（（3 * 60）/ 1））* 100 = 0.00055％任意の時点での衝突の可能性

1000ユーザー=（0.001 /（（3 * 60）/ 1000））* 100 = 0.55％の任意の時点での衝突の可能性

于 2011-02-23T03:26:17.347 に答える