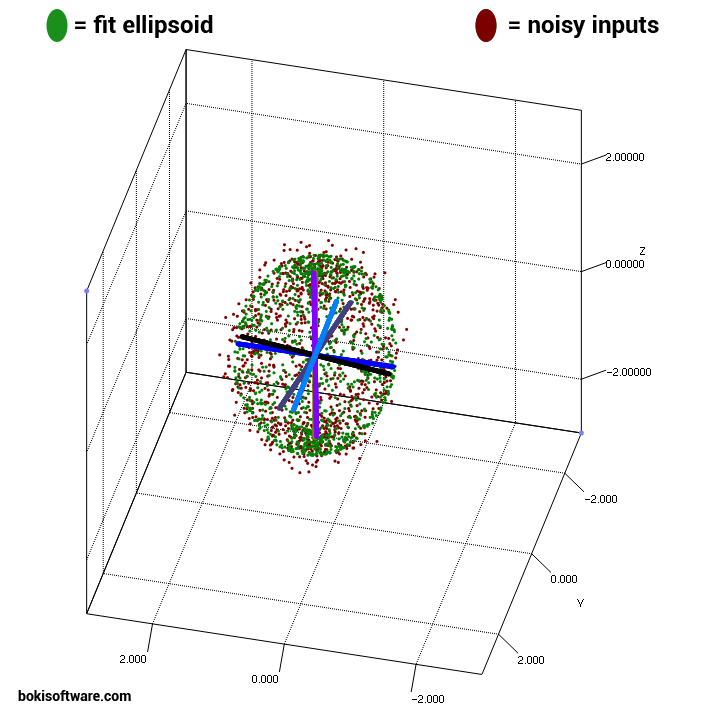
楕円体にフィットさせたい3Dデータポイントの大規模なセットがあります。
私の数学はかなり貧弱なので、数学ライブラリなしで最小二乗法を実装するのに問題があります。
プロジェクトに直接プラグインできるデータに楕円体を適合させることができるコードを知っているか、持っている人はいますか？Cでの使用が最適ですが、C ++、Java、C＃、Pythonなどから変換しても問題ありません。
編集：センターを見つけることができることも大きな助けになるでしょう。ポイントは等間隔ではないため、平均をとっても中心にはなりません。
どうぞ：
この論文では、楕円体の中心を見つけるだけでなく、楕円体を複数の次元に適合させることについても説明します。お役に立てれば、
http://www.physics.smu.edu/~scalise/SMUpreprints/SMU-HEP-10-14.pdf
（ところで、この答えは少し遅れていると思いますが、同じことを探してあなたの質問に出くわした人のために、この解決策を追加すると思いました:)
楕円体を囲む最小ボリュームが必要な場合は、この SO answer for a bounding ellipsoidを確認してください。
最小二乗法で最適な楕円が必要な場合は、平均シフトされた 3D ポイントの共分散行列を見つけ、それを使用して楕円体を作成する誤差楕円体のこの MATLAB コードを確認してください。
楕円体をフィッティングするための適切な Java ベースのアルゴリズムが見つからなかったため、自分で作成することになりました。2D 点を持つ楕円にはいくつかの優れたアルゴリズムがありましたが、3D 点を持つ楕円体には適していませんでした。いくつかの異なる MATLAB スクリプトを試し、最終的に Yury Petrov の Ellipsoid Fit に落ち着きました。楕円体を多項式 Ax^2 + By^2 + Cz^2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz = 1 に適合させます。楕円体を強制するために制約を使用しないため、楕円体の代わりにランダムな quardic が当てはまらないようにするために、かなり多数の点が必要です。それ以外は、非常にうまく機能します。Yury Petrov のスクリプトを Java で実装する Apache Commons Math を使用して、小さな Java ライブラリを作成しました。GIT リポジトリはhttps://github.com/BokiSoft/EllipsoidFitにあります。
最小二乗データ フィッティングは、記述したデータの性質を考えると、おそらく優れた方法論です。GNU Scientific Libraryには、線形および非線形の最小二乗データ フィッティング ルーチンが含まれています。あなたの場合、データを線形空間に変換して線形最小二乗法を使用できる場合がありますが、それは実際のユースケースによって異なります。それ以外の場合は、非線形メソッドを使用する必要があります。
少し前にYuryPetrovの最小二乗MatlabフィッターをJavaに移植しましたが、必要なのはJAMAだけです：https ：//github.com/mdoube/BoneJ/blob/master/src/org/doube/geometry/FitEllipsoid.java
私はちょうど同じプロセスを経験しました。これは、Nima Moshtah の作業に基づく python モジュールです。多くの場所で参照されていますが、バウンディング楕円に関するこの質問でも参照されています
このモジュールは、最終的な楕円体のプロットも処理します。楽しみ！
https://github.com/minillinim/ellipsoid/blob/master/ellipsoid.py
考えがある。おおよその解決策であり、最善ではありませんが、ポイントを内部に保持します。XY 平面で、すべての点を取得する半径 R1 を見つけます。XZ 平面 (R2) と YZ 平面 (R3) についても同様です。次に、各軸で最大値を使用します。A=max(R1,R2)、B=max(R1,R3)、C=max(R2,R3)。しかし、まずすべてのポイントの平均 (中心) を見つけて原点に合わせます。