私が抱えている問題は、XYZ固定軸回転から、Z、X'、Z''の周りのオイラー回転に変換する必要があることです。
関連するマトリックスは次のとおりです。
バツ:
よ:
Z:
Rz(psi) Ry(phi) Rx(theta) = Rxyz(theta,phi,psi); として組み合わせます。彼らは与えます:
Rxyz:
そして、私が望むオイラー角の特定の規則の回転行列。これは:
オイラー:
したがって、私の最初の計画は、行列要素を比較し、その方法で必要な角度を抽出することでした。私はこれを思いつきました(最後に実際の現在のコード):

しかし、これはいくつかの状況では機能しません。最も明白なのは、Cos(theta)Cos(phi) == 1; の場合です。それ以来、Cos(ベータ) = 1、したがってSinβ = 0である。ここで、Sin(ベータ)はコードのs2である。これは、Cos(シータ) と cos(ファイ) = +/- 1 の場合にのみ発生します。
したがって、すぐに考えられる状況を除外することができます。
theta または phi = 0、180、360、540、... の場合、Cos(theta) と Cos(phi) は +/- 1 です。
したがって、これらの場合は別の方法で行う必要があるだけです。
そして、私はこのコードで終わった:
public static double[] ZXZtoEuler(double θ, double φ, double ψ){
θ *= Math.PI/180.0;
φ *= Math.PI/180.0;
ψ *= Math.PI/180.0;
double α = -1;
double β = -1;
double γ = -1;
double c2 = Math.cos(θ) * Math.cos(φ);
β = Math.acos(r(c2));
if(eq(c2,1) || eq(c2,-1)){
if(eq(Math.cos(θ),1)){
if(eq(Math.cos(φ),1)){
α = 0.0;
γ = ψ;
}else if(eq(Math.cos(φ),-1)){
α = 0.0;
γ = Math.PI - ψ;
}
}else if(eq(Math.cos(θ),-1)){
if(eq(Math.cos(φ),1)){
α = 0.0;
γ = -ψ;
}else if(eq(Math.cos(φ),-1)){
α = 0.0;
γ = ψ + Math.PI;
}
}
}else{
//original way
double s2 = Math.sin(β);
double c3 = ( Math.sin(θ) * Math.cos(φ) )/ s2;
double s1 = ( Math.sin(θ) * Math.sin(ψ) + Math.cos(θ) * Math.sin(φ) * Math.cos(ψ) )/s2;
γ = Math.acos(r(c3));
α = Math.asin(r(s1));
}
α *= 180/Math.PI;
β *= 180/Math.PI;
γ *= 180/Math.PI;
return new double[] {r(α), r(β), r(γ)};
}
ここで、r と eq は 2 つの単純な関数です。
public static double r(double a){
double prec = 1000000000.0;
return Math.round(a*prec)/prec;
}
static double thresh = 1E-4;
public static boolean eq(double a, double b){
return (Math.abs(a-b) < thresh);
}
eq はテストのために数値を比較するだけであり、 r は浮動小数点エラーが Math.acos / Math.asin の範囲外の数値をプッシュして NaN の結果を与えるのを防ぐためのものです。
(つまり、時々、私は Math.acos(1.000000000000000004) か何かになってしまいます。)
これは、c2==1 を残す x と y の周りの回転を持つ 4 つのケースを考慮に入れています。
しかし、ここで問題が発生します。
上記で行ったことはすべて意味がありますが、正しい角度が得られません。
ここにいくつかの出力があります。各ペアの最初のものはシータ ファイ psi 角度であり、各ペアの 2 番目は対応するアルファ ベータ ガンマ ラインです。丸め誤差を無視すると、角度の一部が約ずれているようです
[0.0, 0.0, 0.0] - correct!
[0.0, 0.0, 0.0]
[0.0, 0.0, 45.0] - correct!
[0.0, 0.0, 45.0]
[0.0, 0.0, 90.0] - correct!
[0.0, 0.0, 90.0]
[0.0, 0.0, 135.0] - correct!
[0.0, 0.0, 135.0]
[0.0, 0.0, 180.0] - correct
[0.0, 0.0, 180.0]
[0.0, 0.0, 225.0] - correct
[0.0, 0.0, 225.0]
[0.0, 0.0, 270.0] - correct
[0.0, 0.0, 270.0]
[0.0, 0.0, 315.0] - correct
[0.0, 0.0, 315.0]
[0.0, 45.0, 0.0] - incorrect: should be [90, 45, -90]
[90.0, 44.999982, 90.0]
[0.0, 45.0, 45.0]
[45.000018, 44.999982, 90.0]
[0.0, 45.0, 90.0]
[0.0, 44.999982, 90.0]
[0.0, 45.0, 135.0]
[-45.000018, 44.999982, 90.0]
[0.0, 45.0, 180.0]
[-90.0, 44.999982, 90.0]
[0.0, 45.0, 225.0]
[-45.000018, 44.999982, 90.0]
[0.0, 45.0, 270.0]
[0.0, 44.999982, 90.0]
[0.0, 45.0, 315.0]
[45.000018, 44.999982, 90.0]
[0.0, 90.0, 0.0]
[90.0, 90.0, 90.0]
[0.0, 90.0, 45.0]
[45.000018, 90.0, 90.0]
[0.0, 90.0, 90.0]
[0.0, 90.0, 90.0]
[0.0, 90.0, 135.0]
[-45.000018, 90.0, 90.0]
[0.0, 90.0, 180.0]
[-90.0, 90.0, 90.0]
[0.0, 90.0, 225.0]
[-45.000018, 90.0, 90.0]
Math.acos と Math.asin の仕組みによるものだと思います。解決策を考えられる人はいますか?
編集: math.asin と math.acos は、それぞれ -pi/2 と pi/2 および 0 と pi の間の値を返します。これは曖昧ではないので、ここに問題があるとは思いません。どこかで数学が間違っているようですが、私の推論に穴が見当たりません...
EDIT2:オイラー回転がどのように機能するかを知らない人には、次のようになります:
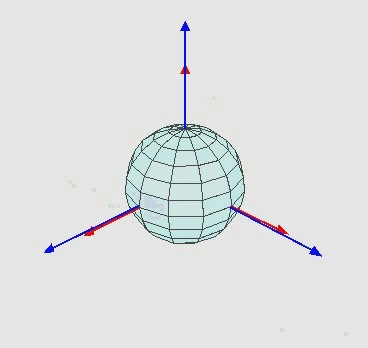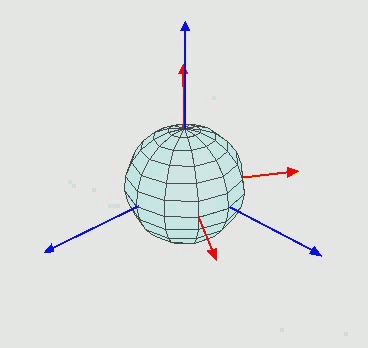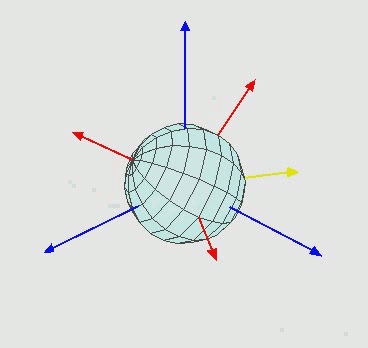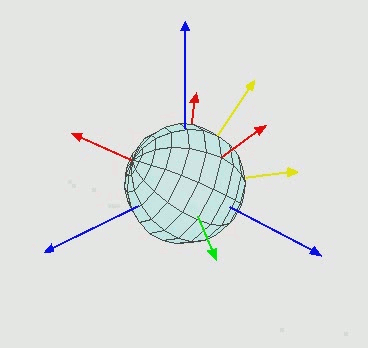
つまり、Zを中心に回転し、次に新しいX軸 ( X' ) を中心に、次に新しいZ''軸を中心に回転します。