問題タブ [quad]

この関数を Python に統合しようとしています。

I = 積分(積分( g(y) * ln[f(x,y)/g(y)] dx) dy) ここで、g(y) = 0 から 1 までの積分(f(x,y)dx)

しかし、コードを実行すると、"g" が定数で、"I" が負であることがわかりました。quad 関数の使い方が間違っていますか? どのように g を定数にすることができますか?

数値を取り、それを積分のパラメーターとして使用し、積分の結果を返す関数をプロットしたいと考えています。単一の浮動小数点数を入力すると、関数は問題なく値を返します。しかし、numpy.linspace(0,3,500) のようなものを指定すると、関数内の "quad" モジュールの応答が悪くなります。

配列の方が優れているという理由だけで、代わりに「nquad」を使用するというアドバイスを調べました。さらに、ドキュメントを読んでエラーを調べましたが、どの例/解決策も私の特定の状況に関係していないようです。

これが私の関数と、それらを実行したときに発生するエラーです。

quad: "提供された関数は有効な float を返しません"

nquad: "quad" と同じエラーです。今回は、自立型のコード全体を示します。単一の浮動小数点数を使用した関数の使用を含めました。

出力が数値ではなく新しい関数である Python を使用して関数を統合したいと考えています。たとえば、次の方程式があります (Arnett 1982 から -- 超新星の分析的説明)。

次に、A の積分を見つけて、結果をプロットします。まず、単純に scipy.quad を試しました。

ここで、B も定義済みの関数です (ここでは示されていません)。A と B はどちらも z の関数ですが、最終的な式は時間 t の関数です。（ここでコードが失敗する原因になっていると思います。）

A と B の積分はゼロから x まで実行されます。x は時間 t の関数です。このままコードを実行しようとすると、「ValueError: 複数の要素を持つ配列の真の値があいまいです。a.any() または a.all() を使用してください」というエラーが表示されます。

そのため、少し検索した後、sympy が適しているのではないかと思いました。しかし、私もこれで失敗しています。

このタスクを完了する方法を教えてください。

どうもありがとう、ザック

これは簡単な質問かもしれませんが、クアッド統合でノード数を増やそうとしています。これに関する関連ドキュメントが見つかりませんでした。

ほとんどがゼロですが、非常に狭い間隔で非ゼロの 1 次元関数 (ディラック デルタのような) があります。そのため、適応クワッドはその間隔をキャッチできず、ゼロを返します。より多くのポイントでサンプリングして、そのピークを捉えようとしています。これどうやってやるの？SciPy のドキュメントはあまり語っていません。

この狭いピークの位置が変わります。ピークの正確な位置はわかりません。

積分 t= \int_{0}^{z} 1/sqrt(2*(0.46732451-z**2)) の上限を解こうとしているため、この関数をプロットすると、次のようにE=0.46732451なります.t=1.07589765

その周りt=1は一種の漸近線です。

次のコードがあります

しかし、このコードは、何を入れても推測値を出力するだけなので、曲線がそこに漸近するという事実と関係があると推測しています。tこのコードは、漸近領域から離れた 他の値に対しても機能することに注意してください。

誰でもこれを解決するのを手伝ってもらえますか?

ありがとう

編集しばらく遊んだ後、問題を解決しましたが、それは一種のパッチワークであり、一般的ではない同様の問題に対してのみ機能します（またはそうですか？）

次の変更を加えました:z到達できる最大値は です。そのため、 からの間の任意の場所sqrt(0.46732451)に設定x0=0.5*np.sqrt(0.46732451)して設定すると、正解がポップされます。これについての説明はありません。おそらく、この問題の専門家である誰かが助けてくれますか? factor0.11

(-x または 0) -> 無限大からの積分について、MATLABquadgkと Python のルーチンの間で一貫性のない結果が得られます。quadMATLAB バージョンは (パラメーターを 1 から -1 に切り替えるセンス チェックに基づいて) 正しいと思いますがflag、Python バージョンは誤った結果 (この場合は 0) を返します。MATLAB は 0.1022 を生成します。これらintegrandsは同一であり、xMATLAB によって生成された値quadgkを Python に挿入することも含め、各ステップを結び付けました (その結果、Python バージョンは MATLAB と同じ値を生成し、それらをintegrand関数に渡すだけです)。この時点で、SciPy ではなく、Gauss-Legendre 求積法 ( https://sourceforge.net/projects/fastgausslegendrequadrature/ ) などの別のルーチンを使用することを検討しています。しかし、それを a/b 範囲から -a->infinity に拡張する方法がわかりません (有限数にしか到達しないこれらの方法を見てきました:

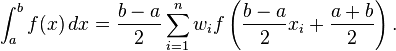numpy での Gauss-Legendre 求積の間隔が異なるのに対し、b=np.Inf結果はNaN. また、変換を読んでいますが、返されたノードと重みから統合をセットアップする方法もわかりませんが、 a と b の有限範囲のみです: https://pomax.github.io/bezierinfo/legendre-gauss.htmlどちらかそれまたは誰かがこれを処理できる Python ライブラリを知っている場合 - quad600,000 個の関数をすばやく統合する必要があるため (つまり、C++ ライブラリへのリンク上記リンク）。ここで本当に奇妙なのは、上に移動して同じ結果を得ることができたことです。volPython の結果は 0 で崩壊します。非常に紛らわしいです。微積分から何年も経ちました...ここにPythonコードがあります：

MATLAB コードは次のとおりです ( integrand.M として保存する必要があり、コマンド ウィンドウにスクリプトを入力できます)。

% スクリプト部分

MATLAB と Python は、代わりにこれらの入力が渡された場合 (変数の上で転置)、クワッドを使用して同じ結果を生成することに注意してください。

Python で quad() の実行時間を短縮する必要があります (数千の積分を統合しています)。ここで、いくつかの統合を行い、部分的な値を追加することを提案した同様の質問を見つけました。ただし、パフォーマンスは向上しません。何かご意見は？簡単な例を次に示します。

これは、単純な積分が 1 であるべきだと私が考えるケースですが、dblquad は頑固に 0.81 と言っています。

詳細: 以下の関数 createFun は、実際の関数を返します。[-b, 1-a] の値を取る確率変数の密度関数を意図した、区分線形です。

ここで、特定の値 a=0 および b=0.2 に対して、そのような関数を 1 つ作成します。

まず、[-b, 1-a] の積分が本当に 1 であることを確認します。

ここまでは順調です。ここで、関数 g:RxR --> R を g(y,x) = f1(x) * f1(y) として定義します。

平方 [-b, 1-a] x [-b, 1-a] における g の二重積分は、各変数の積分の積になるはずです (g は x と a の関数として因数分解されます)。 y の関数)、どちらも 1 であるため、1*1=1 と予想しました。しかし、コード

は 0.8161 を示しており、1E-10 のオーダーの非常に低いエラーがあります。

私の数学は間違っていますか?何らかの理由でこの積分は 1 ではありませんか? それともそうですが、dblquad を正しく使用していませんか? では、どのようにすればよいのでしょうか。