問題タブ [rotational-matrices]

OpenGLでオブジェクト（惑星）を現在のカメラの回転に対して回転させるのに問題があります。最初は機能しているように見えますが、少し回転させた後、回転はカメラに対して正しく/相対的ではなくなります。

画面上のmouseXとmouseYの動きのデルタ（差）を計算しています。回転は「planetRotation」と呼ばれるVector3Dに保存されます。

これがplanetRotationを基準にした回転を計算するための私のコードです：

理論的には、これは、「rotateAmount」変数に回転を設定します。次に、このベクトルに逆モデル変換行列（rotMatrix）を乗算することにより、これをモデル空間に取り込みます。

次に、この変換された回転が現在の回転に追加されます。

これをレンダリングするには、セットアップ中のトランスフォームを使用します。

カメラのようなぐらつき、私が実行しようとしている回転は、現在の変換に対して相対的ではないようです。

私は何が間違っているのですか？

私は物理学者であり、いくつかのプログラミングを学んでおり、行列/ベクトル形式で物事を書く代わりに、回転にクォータニオンを使用している多くの人々に出くわしました。

物理学では、クォータニオンを使用しない非常に良い理由があります（ハミルトン/ギブスなどについて時々語られる奇妙な話にもかかわらず）。物理学では、説明に優れた分析動作が必要です（これは正確に定義された意味を持ちますが、通常のイントロクラスで教えられるものをはるかに超える技術的な方法であるため、詳細には触れません）。クォータニオンにはこのような優れた動作がないことが判明したため、それらは有用ではなく、ベクトル/行列は有用であるため、これらを使用します。

ただし、解析構造を使用しない厳密な回転と記述に限定して、3D回転はどちらの方法（または他のいくつかの方法）でも同等に記述できます。

^{一般に、X 2} = X ' ²という制約に従って、点X =（x、y、z）を新しい点X'=（x'、y'、z'）にマッピングする必要があります。そして、これを行うことはたくさんあります。

素朴な方法は、これが定義する三角形を描画して三角法を使用するか、点（x、y、z）とベクトル（x、y、z）の間の同型写像と関数f（X）=X'を使用することです。行列MX=X'、またはクォータニオンを使用する、または他の方法（x、y、z）^T。（a、b、c）（x'、y'、 z'）など。

数学の観点から、これらの説明はすべてこの設定で同等です（定理として）。それらはすべて、同じ数の自由度、同じ数の制約などを持っています。

では、なぜクォータニオンがベクトルよりも優先されるように見えるのでしょうか。

私が見る通常の理由は、ジンバルロックや数値の問題ではありません。

これはオイラー角の問題にすぎないため、ジンバルロックなしの議論は奇妙に思えます。これは座標の問題でもあり（極座標のr = 0での特異点（ジャコビアンはランクを失う）のように）、これは局所的な問題であり、座標を切り替えて縮退から回転することで解決できます。または2つの重なり合う座標系を使用します。

これらの両方（および代替案）がどのように実装されるかについては詳細にわからないため、数値の問題についてはよくわかりません。クォータニオンの再正規化は、回転行列の場合よりも簡単であることを読みましたが、これは一般的な行列の場合にのみ当てはまります。回転には、これを簡単にする追加の制約があります（これは、クォータニオンの定義に組み込まれています）（実際、自由度が同じであるため、これは真である必要があります）。

では、ベクトルや他の代替手段よりもクォータニオンを使用する理由は何ですか？

少し前にこれを twitter に投稿しましたが、私のフォロワーの誰も数学/プログラミングの天才ではないように見えるので、ここでも運試しをします. 私のソリューションの一部が含まれている可能性があるこれを見つけたので、ここに来ました。

私が達成しようとしているものの写真を含む、次のpdfドキュメントで私の問題を説明しました。

さらに詳細を説明するために、12 面体の五角形 (12 個の五角形) を三角形 (5 個/五角形、合計 60 個の三角形) に分割し、これらの各三角形に関連する一連のデータ ポイントを収集しました。

アイデアは、個々の三角形ごとに地形メッシュを生成することです。そのためには、データを 32K x 32K の正方形 (idTech4 Megatexture) でフラットに表現する必要があります。

変換マトリックスについて漠然と聞いたことがありますが、適切に設定すると、すべてのデータポイントを通過させて適切な場所に表示させることができます。

私はこのソースコードをここで見ましたが、そこにポイントを出し入れする方法がわかりません。セットアップを行う方法は言うまでもなく、各ポイントを順番に提示して結果を取得する方法は言うまでもありません振り返る。

右後ろの隅にあるポイントを特定するのと同じくらい速くなりました。すべての 3D ポイントは、もともと緯度/経度のペアで保存されています。この方法で 3D ベクトルを取得します。

私の考えでは、三角形の中心を見つけることができ、球の中心から三角形の中央までのベクトルが 90N に移動するように角度をオフセットする方法を発見できれば、ポイントはすでに適切な平面にあると考えられます。それらをすべて同じ角度に沿って回転させました。次に、それらをすべて 3D に変換し、y から半径を差し引くと、正しい y 位置にもなります。

あとは、回転、スケーリング、および最終位置への移動だけです。

三角形にはいくつかの種類の「中心」があります。私が必要とするのは、三角形の角から等距離にあるものだと思います (外心?)

しかし、問題全体へのより簡単なアプローチがあるかもしれないので、私が自分の研究を続けている間、おそらくあなたの何人かが私を正しい方向に向けるのを助けることができます.

いくつかのサンプル データが用意されているように見えます。これらの三角形のいくつかを obj ファイル形式で示します。

そして別：

各ポイントが 0,0,0 から 3396 の距離にあることに気付くでしょう。「球上」と言いました。これは、球の中心から離れた面が、変換されたときに「上」になる必要がある面であることを意味します。広場。

理論的には、これらすべての三角形は実際には同じサイズである必要がありますが、それらを生成した数学の丸め誤差により、これが完全に正しいとは限りません。

私が間違っていなければ、ここに表示される最初のポイントが常に最も長い境界線の反対側にあることを確認するための対策を既に講じているため、左端隅に配置する必要があります (上記の 2 つのサンプルをテストすると、これが確認されますが、とにかく念のために測定しています)この点から離れた両方の脚も理論的には同じ長さである必要がありますが、丸め誤差がそれをわずかに相殺する可能性があります.

私が正しくやった場合、長い辺は 2 つの短い辺よりも 1,113587 倍長くなります。それらが同一であると仮定して、Excel でいくつかのゴール シークを行うと、この三角形を翻訳しただけであると仮定すると、最終的なポイントは次のようになると推測できます。

したがって、以下で説明するように、できれば 4x4 マトリックスを使用して、この変換を行うようにマトリックスをセットアップする必要があります。

I am trying to recover the 3D orientation of the three axes of a building in an image.

My current approach is to manually annotate the three vanishing points corresponding to the three axes, estimate the camera calibration matrix K, and then compute each column of the rotation matrix from a vanishing point by normalising K^{-1}v_{i}, as outlined in the appendix of this paper.

Although this seems to work, the computed columns of R are not completely orthogonal, and I suspect the problem would be even more pronounced if the vanishing points are more noisy.

I could fudge it by decomposing the estimated R using SVD and setting all singular values to 1, but I would prefer a more principled solution. Another line of thought is to solve it as a constrained optimisation problem that seeks to minimise projection error on the vanishing points.

Is there a better way of computing the rotation matrix from K and the vanishing points, that simultaneously take into account of orthogonality and column unity constraints?

Thanks in advance.

キャンバスを作成してその上にビットマップを描画し、キャンバスに触れるたびにアニメーション化します

描画の開始時にビットマップの境界を設定しましたが、回転行列を変更してビットマップを回転した後、新しい行列に基づいて境界が変更されません

ビットマップをクリック可能なオブジェクトとして使用し、クリックするとイベントを発生させるには、ビットマップの境界をリセットする必要があります。

回転行列に基づいて境界を更新するにはどうすればよいですか？

前もって感謝します

スピードメーターをプログラムして、後で GPS データなどを入力しようとしています。針 (480x480) をソースとして表示し、速度計を背景画像 (480x480) として表示する ImageView があります。ここで、次のコードで針を回転させてみます: (1 単位 [km/h] は 2.25° の角度です)

それは今のところうまくいきます。しかし、針が回っている間、レイアウトのサイズは妥協します. 写真の対角線が高さよりも大きく、マトリックスを回転させている間、レイアウトがその高さいっぱいまで伸びているためだと思います (これは対角線です)。だから私のスピードメーターは常に変化しています。私にできることはありますか？

私が抱えている問題は、XYZ固定軸回転から、Z、X'、Z''の周りのオイラー回転に変換する必要があることです。

関連するマトリックスは次のとおりです。

バツ：

よ:

Z:

Rz(psi) Ry(phi) Rx(theta) = Rxyz(theta,phi,psi); として組み合わせます。彼らは与えます：

Rxyz:

そして、私が望むオイラー角の特定の規則の回転行列。これは：

オイラー:

したがって、私の最初の計画は、行列要素を比較し、その方法で必要な角度を抽出することでした。私はこれを思いつきました（最後に実際の現在のコード）：

しかし、これはいくつかの状況では機能しません。最も明白なのは、Cos(theta)Cos(phi) == 1; の場合です。それ以来、Cos(ベータ) = 1、したがってSinβ = 0である。ここで、Sin(ベータ)はコードのs2である。これは、Cos(シータ) と cos(ファイ) = +/- 1 の場合にのみ発生します。

したがって、すぐに考えられる状況を除外することができます。

theta または phi = 0、180、360、540、... の場合、Cos(theta) と Cos(phi) は +/- 1 です。

したがって、これらの場合は別の方法で行う必要があるだけです。

そして、私はこのコードで終わった：

ここで、r と eq は 2 つの単純な関数です。

eq はテストのために数値を比較するだけであり、 r は浮動小数点エラーが Math.acos / Math.asin の範囲外の数値をプッシュして NaN の結果を与えるのを防ぐためのものです。

(つまり、時々、私は Math.acos(1.000000000000000004) か何かになってしまいます。)

これは、c2==1 を残す x と y の周りの回転を持つ 4 つのケースを考慮に入れています。

しかし、ここで問題が発生します。

上記で行ったことはすべて意味がありますが、正しい角度が得られません。

ここにいくつかの出力があります。各ペアの最初のものはシータ ファイ psi 角度であり、各ペアの 2 番目は対応するアルファ ベータ ガンマ ラインです。丸め誤差を無視すると、角度の一部が約ずれているようです

Math.acos と Math.asin の仕組みによるものだと思います。解決策を考えられる人はいますか?

編集: math.asin と math.acos は、それぞれ -pi/2 と pi/2 および 0 と pi の間の値を返します。これは曖昧ではないので、ここに問題があるとは思いません。どこかで数学が間違っているようですが、私の推論に穴が見当たりません...

EDIT2：オイラー回転がどのように機能するかを知らない人には、次のようになります：

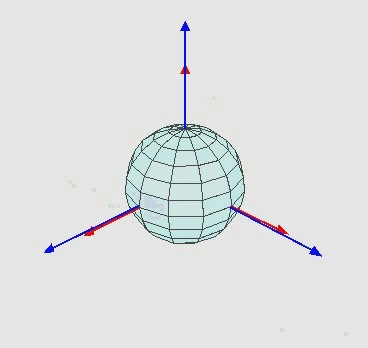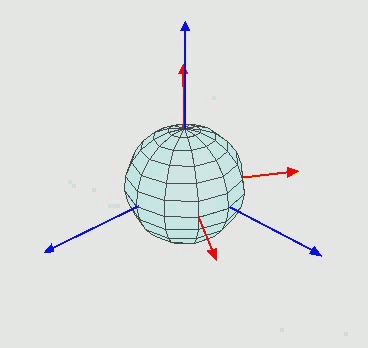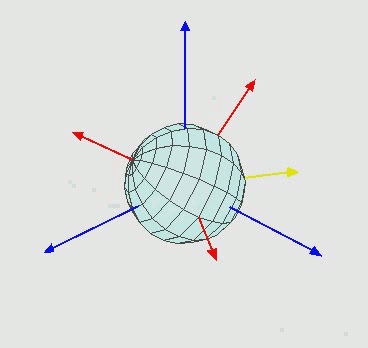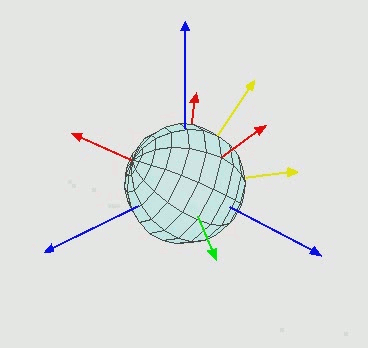
つまり、Zを中心に回転し、次に新しいX軸 ( X' ) を中心に、次に新しいZ''軸を中心に回転します。

そのため、SensorEventのドキュメントを調べて、電話の特定の軸を基準にして、北の方向を把握する方法を理解しようとしています。座標系がどのように機能するかについての私の概念を説明する小さな画像を描きました。

したがって、世界座標がx、y、zであり、磁北がzに沿っており、yが空を指し、電話の座標がPx、Py、Pzである場合、投影を計算できるようにしたいと思います。各ベクトルを他のベクトルに変換します。

SENSOR_TYPE_ROTATION_VECTORは正しいもののように見えますが、これらすべての予測を取得するのに十分な情報が得られていないようです。ROTATION_VECTORを正規化し、それを気になる軸に追加してから、コンポーネントを引き出すことになっていますか？

もう1つの大きな単一センサーはSENSOR_TYPE_ORIENTATIONのようですが、これらの値をどう処理するかがわかりません。実世界の座標系のPyへの3つの投影を知りたい場合は、次のように、指定された座標に沿って[0、1、0]を回転します。

一般的な回転の式からこれらの式を取得したところ（単位ベクトルを回転しているため、中央の列を選択するだけです）。変数Pyの成分は、x、y、zのPyへの射影になると思いますが、それは逆になりますか？代わりに、3つの実世界の軸のそれぞれへのPyの投影ですか？

最後に、getRotationMatrixFromVector（）オプションがあることに気づきました。これは、これらの予測を計算するように見えますが、完全に逆方向にあるかどうかはわかりません。xの3つの射影を知りたい場合。yとzをPyに追加しますが、回転行列の2番目の列、または2番目の行を取得しますか？

（おそらく非常に単純な質問の非常に言葉の多いバージョンについては申し訳ありませんが、将来の混乱している人々にとっては、私の主要な混乱のポイントである座標系について非常に明確にする方が良いと思います）。

jPCT ライブラリを使用して FPS に取り組んでいます。すべての FPS に必要な重要な点の 1 つは、マウスを上下に動かしすぎてプレイヤーが背後を見ないようにすることです。現在、jPCT の Web サイトにあるサンプル コードを使用して、カメラに追加された角度を追跡していますが、すべての角度をラジアンで丸める問題が心配です。jPCT のカメラから回転マトリックスを取得できます。これには、プレーヤーがどの程度「高い」位置にあるかを把握するための情報が含まれていることはわかっていますが、マトリックスからそれを取得する方法がわかりません。

プレイヤーが真上よりも「上」を向いているか、真下よりも「下」を向いているかを教えてくれる回転マトリックスで何を探すでしょうか?

任意の4x4変換行列が与えられた場合、回転の中心を見つけるにはどうすればよいですか？